



suivant: Régime non linéaire
monter: Développement P 1
précédent: Développement P 1
Table des matières
En l'absence d'effet Ehrlich-Schwoebel (
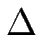
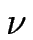 = 0) et en négligeant les interactions élastiques (
= 0) et en négligeant les interactions élastiques (
 = 0), la partie réelle de
= 0), la partie réelle de  se récrit :
se récrit :
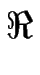 e( e(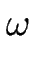 ) = P ) = P 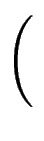  + +  P P (1 - cos( (1 - cos(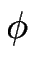 ))(cos( ))(cos(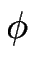 ) - cos( ) - cos( )) ))
|
(A.27) |
Le mode le plus instable  est donné par :
est donné par :
cos( ) = ) =  (1 + cos( (1 + cos( )) = )) =  . .
|
(A.28) |
Pour 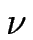
 1, nous obtenons
1, nous obtenons


 /2 +
/2 + 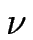 /2 alors que pour
/2 alors que pour 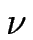
 1, nous avons
1, nous avons

 2/
2/ .
Ainsi, si les coefficients cinétiques sont faibles (i.e. pour un processus de croissance limité par la cinétique d'attachement, comme dans le cas des expériences de croissance de macromolécules réalisées par Chernov et al. [#!Chernov97!#] [#!Coriell98!#]), le mode le plus instable correspond pratiquement à un déphasage entre marches de
.
Ainsi, si les coefficients cinétiques sont faibles (i.e. pour un processus de croissance limité par la cinétique d'attachement, comme dans le cas des expériences de croissance de macromolécules réalisées par Chernov et al. [#!Chernov97!#] [#!Coriell98!#]), le mode le plus instable correspond pratiquement à un déphasage entre marches de
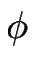 =
=  /2 (et non
/2 (et non 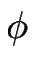 =
=  comme c'est souvent le cas dans les instabilités de mise en paquets).
De telles instabilités avec un tel déphasage de
comme c'est souvent le cas dans les instabilités de mise en paquets).
De telles instabilités avec un tel déphasage de  /2 ont déjà été rencontrées dans le cas de l'électromigration avec un courant électrique parallèle aux marches [#!Liu98a!#], mais l'instabilité résultante est différente de celle-ci car cette dernière se produit durant la croissance.
/2 ont déjà été rencontrées dans le cas de l'électromigration avec un courant électrique parallèle aux marches [#!Liu98a!#], mais l'instabilité résultante est différente de celle-ci car cette dernière se produit durant la croissance.
Cette valeur singulière du déphasage entre marches pour le mode le plus instable implique que la pulsation du mode le plus instable possède une partie imaginaire non nulle. Cette nouvelle instabilité est donc
dans cette limite, oscillante dans le temps.




suivant: Régime non linéaire
monter: Développement P 1
précédent: Développement P 1
Table des matières
fred
2001-07-02
![]()
![]() = 0) et en négligeant les interactions élastiques (
= 0) et en négligeant les interactions élastiques (
![]() = 0), la partie réelle de
= 0), la partie réelle de ![]() se récrit :
se récrit :
 +
+  .
.