



suivant: Conservation de la masse
monter: Modélisation de la dynamique
précédent: Diffusion sur les terrasses
Table des matières
L'équation différentielle [![[*]](crossref.gif) ] décrivant les variations du champ de concentration cm étant du second ordre, elle fait intervenir deux constantes d'intégration.
Pour pouvoir déterminer le champ de concentration cm sur la terrasse m, il nous faut donc deux équations supplémentaires. Elles nous sont données par la description du comportement du champ de concentration aux extrémités de la terrasse et fournissent ainsi deux conditions aux limites. Dans le modèle BCF initial, la concentration d'adatomes était considérée à l'équilibre thermodynamique, au bord des marches. Pour la description de la dynamique, hors de l'équilibre, de la surface vicinale, il faut relaxer cette hypothèse. Les conditions aux limites sont traduites par une relation linéarisée « à la Onsager » , reliant les flux de matière à l'écart par rapport à l'équilibre :
] décrivant les variations du champ de concentration cm étant du second ordre, elle fait intervenir deux constantes d'intégration.
Pour pouvoir déterminer le champ de concentration cm sur la terrasse m, il nous faut donc deux équations supplémentaires. Elles nous sont données par la description du comportement du champ de concentration aux extrémités de la terrasse et fournissent ainsi deux conditions aux limites. Dans le modèle BCF initial, la concentration d'adatomes était considérée à l'équilibre thermodynamique, au bord des marches. Pour la description de la dynamique, hors de l'équilibre, de la surface vicinale, il faut relaxer cette hypothèse. Les conditions aux limites sont traduites par une relation linéarisée « à la Onsager » , reliant les flux de matière à l'écart par rapport à l'équilibre :
- 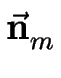 . . 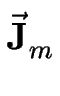 (zm) (zm) |
= |
  cm(zm) - ceqm cm(zm) - ceqm![$\displaystyle \left.\vphantom{ c_m(z_m) - c_{eq_m} }\right]$](img66.gif) , , |
(2.3) |
 . . 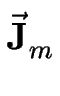 (zm + 1) (zm + 1) |
= |
  cm(zm + 1) - ceqm + 1 cm(zm + 1) - ceqm + 1![$\displaystyle \left.\vphantom{ c_m(z_{m+1}) - c_{eq_{m+1}} }\right]$](img70.gif) , , |
(2.4) |
où
 est le flux de matière sur la terrasse m (
est le flux de matière sur la terrasse m (
 (zm) est sa valeur au bord de la marche m) et
(zm) est sa valeur au bord de la marche m) et
 est le vecteur normal à la marche m, pointant pour une marche droite, dans le sens descendant les marches. On a :
où, par commodité, nous avons utilisé la notation
est le vecteur normal à la marche m, pointant pour une marche droite, dans le sens descendant les marches. On a :
où, par commodité, nous avons utilisé la notation
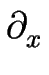 pour signifier
pour signifier
 /
/ x (cette notation sera couramment utilisée dans la suite de la thèse).
ceqm est la valeur à l'équilibre thermodynamique de la concentration d'adatomes au bord de la marche m ;
(cm(zm) - ceqm) mesure donc l'écart par rapport à l'équilibre.
x (cette notation sera couramment utilisée dans la suite de la thèse).
ceqm est la valeur à l'équilibre thermodynamique de la concentration d'adatomes au bord de la marche m ;
(cm(zm) - ceqm) mesure donc l'écart par rapport à l'équilibre.
 et
et  sont des coefficients traduisant la cinétique d'attachement des adatomes aux marches.
Une valeur infinie de
sont des coefficients traduisant la cinétique d'attachement des adatomes aux marches.
Une valeur infinie de  traduit un attachement instantané aux marches (dans ce cas
cm = ceqm) alors qu'une valeur nulle rend compte d'un attachement impossible (dans ce cas le flux de matière arrivant en bord de terrasse est nul :
traduit un attachement instantané aux marches (dans ce cas
cm = ceqm) alors qu'une valeur nulle rend compte d'un attachement impossible (dans ce cas le flux de matière arrivant en bord de terrasse est nul :
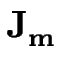 = 0).
L'effet Ehrlich-Schwoebel présenté en introduction est pris en compte en prenant
= 0).
L'effet Ehrlich-Schwoebel présenté en introduction est pris en compte en prenant
 >
>  . On utilisera souvent dans la suite la différence de cinétique d'attachement
. On utilisera souvent dans la suite la différence de cinétique d'attachement
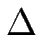
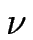 =
=  -
-  qui caractérise l'importance de l'effet Ehrlich-Schwoebel.
On définit aussi les longueurs Schwoebel d± par :
d± =
qui caractérise l'importance de l'effet Ehrlich-Schwoebel.
On définit aussi les longueurs Schwoebel d± par :
d± =  /D ; c'est la distance moyenne supplémentaire que parcourt un adatome lors de ses tentatives d'attachement.
Au bord de la marche m, le flux de matière
/D ; c'est la distance moyenne supplémentaire que parcourt un adatome lors de ses tentatives d'attachement.
Au bord de la marche m, le flux de matière
 s'écrit :
s'écrit :
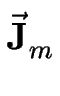 (zm) = - (zm) = -  D D  cm (zm) + cm (zm) +  cm(zm) cm(zm)![$\displaystyle \left.\vphantom{ D \, \vec{\bf\nabla} c_m \, (z_m) + \vec{\bf V}_m \, c_m(z_m) }\right]$](img90.gif) , ,
|
(2.6) |
où
 est la vitesse de la marche m.
Le premier terme décrit le flux de matière provenant de la diffusion des adatomes. Le second terme traduit l'existence d'un flux effectif de matière dû au fait que la marche se déplace dans le champ de diffusion cm avec une vitesse
est la vitesse de la marche m.
Le premier terme décrit le flux de matière provenant de la diffusion des adatomes. Le second terme traduit l'existence d'un flux effectif de matière dû au fait que la marche se déplace dans le champ de diffusion cm avec une vitesse
 . Conformément à la remarque faite plus haut, cet effet advectif étant négligeable dans les conditions expérimentales usuelles2.4, nous n'en tiendrons pas compte par la suite ; les conditions aux limites prennent alors la forme suivante :
. Conformément à la remarque faite plus haut, cet effet advectif étant négligeable dans les conditions expérimentales usuelles2.4, nous n'en tiendrons pas compte par la suite ; les conditions aux limites prennent alors la forme suivante :
D 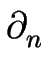 cm(zm) cm(zm) |
= |
  cm(zm) - ceqm cm(zm) - ceqm![$\displaystyle \left.\vphantom{ c_m(z_m) - c_{eq_m} }\right]$](img66.gif) , , |
(2.7) |
D 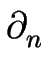 cm(zm + 1) cm(zm + 1) |
= |
-   cm(zm + 1) - ceqm + 1 cm(zm + 1) - ceqm + 1![$\displaystyle \left.\vphantom{ c_m(z_{m+1}) - c_{eq_{m+1}} }\right]$](img70.gif) , , |
(2.8) |
où
 c =
c =  .
.  c est la dérivée de c dans la direction normale
c est la dérivée de c dans la direction normale
 .
.




suivant: Conservation de la masse
monter: Modélisation de la dynamique
précédent: Diffusion sur les terrasses
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ] décrivant les variations du champ de concentration cm étant du second ordre, elle fait intervenir deux constantes d'intégration.
Pour pouvoir déterminer le champ de concentration cm sur la terrasse m, il nous faut donc deux équations supplémentaires. Elles nous sont données par la description du comportement du champ de concentration aux extrémités de la terrasse et fournissent ainsi deux conditions aux limites. Dans le modèle BCF initial, la concentration d'adatomes était considérée à l'équilibre thermodynamique, au bord des marches. Pour la description de la dynamique, hors de l'équilibre, de la surface vicinale, il faut relaxer cette hypothèse. Les conditions aux limites sont traduites par une relation linéarisée « à la Onsager » , reliant les flux de matière à l'écart par rapport à l'équilibre :
] décrivant les variations du champ de concentration cm étant du second ordre, elle fait intervenir deux constantes d'intégration.
Pour pouvoir déterminer le champ de concentration cm sur la terrasse m, il nous faut donc deux équations supplémentaires. Elles nous sont données par la description du comportement du champ de concentration aux extrémités de la terrasse et fournissent ainsi deux conditions aux limites. Dans le modèle BCF initial, la concentration d'adatomes était considérée à l'équilibre thermodynamique, au bord des marches. Pour la description de la dynamique, hors de l'équilibre, de la surface vicinale, il faut relaxer cette hypothèse. Les conditions aux limites sont traduites par une relation linéarisée « à la Onsager » , reliant les flux de matière à l'écart par rapport à l'équilibre :
