



suivant: Solution stationnaire du train
monter: Modélisation de la dynamique
précédent: Relations cinétiques d'attachement aux
Table des matières
Si la conformation du train de marche est connue, les équations [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] permettent de déterminer le champ de concentration cm sur la terrasse m.
Malheureusement, la géométrie du train de marches est a priori indéterminée. C'est un problème de frontière libre : la géométrie des marches détermine le champ de concentration sur les terrasses mais la dynamique de ces marches dépend elle-même du champ de concentration d'adatome à la surface 2.5.
Il nous faut donc une équation supplémentaire pour décrire la dynamique de la marche m. Elle nous est donnée par une équation de conservation de la matière au niveau de la marche m, qui traduit que l'avancée de celle-ci est proportionnelle au bilan des flux incidents de matière :
] permettent de déterminer le champ de concentration cm sur la terrasse m.
Malheureusement, la géométrie du train de marches est a priori indéterminée. C'est un problème de frontière libre : la géométrie des marches détermine le champ de concentration sur les terrasses mais la dynamique de ces marches dépend elle-même du champ de concentration d'adatome à la surface 2.5.
Il nous faut donc une équation supplémentaire pour décrire la dynamique de la marche m. Elle nous est donnée par une équation de conservation de la matière au niveau de la marche m, qui traduit que l'avancée de celle-ci est proportionnelle au bilan des flux incidents de matière :
 . .  = =   . .   (zm) - (zm) - 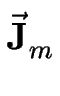 (zm) (zm)![$\displaystyle \left.\vphantom{ \vec{\bf J}_{m-1}(z_m) - \vec{\bf J}_m(z_m) }\right]$](img100.gif) - a - a 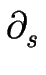  , ,
|
(2.9) |
où a est le paramètre de maille du réseau cristallin et
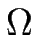 = a2, s est l'abscisse curviligne le long de la marche et
= a2, s est l'abscisse curviligne le long de la marche et
 =
=  .
.  est la dérivation dans la direction tangentielle à la marche
est la dérivation dans la direction tangentielle à la marche
 .
.
 est un flux de matière provenant de la diffusion le long du bord de marche ( « diffusion de ligne » ) et s'écrit [#!Ihle98!#] :
où DL est le coefficient de diffusion de ligne [#!Mullins57!#], [#!Ihle98!#],
est un flux de matière provenant de la diffusion le long du bord de marche ( « diffusion de ligne » ) et s'écrit [#!Ihle98!#] :
où DL est le coefficient de diffusion de ligne [#!Mullins57!#], [#!Ihle98!#], 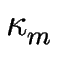 est la courbure de la marche m, définie positive pour une marche convexe et
est la courbure de la marche m, définie positive pour une marche convexe et 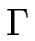 est relié à la rigidité de ligne
est relié à la rigidité de ligne
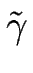 par :
par :
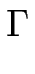 = =  . .
|
(2.11) |
Les équations [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] décrivent complètement la dynamique du train de marches 2.6.
] décrivent complètement la dynamique du train de marches 2.6.




suivant: Solution stationnaire du train
monter: Modélisation de la dynamique
précédent: Relations cinétiques d'attachement aux
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] permettent de déterminer le champ de concentration cm sur la terrasse m.
Malheureusement, la géométrie du train de marches est a priori indéterminée. C'est un problème de frontière libre : la géométrie des marches détermine le champ de concentration sur les terrasses mais la dynamique de ces marches dépend elle-même du champ de concentration d'adatome à la surface 2.5.
Il nous faut donc une équation supplémentaire pour décrire la dynamique de la marche m. Elle nous est donnée par une équation de conservation de la matière au niveau de la marche m, qui traduit que l'avancée de celle-ci est proportionnelle au bilan des flux incidents de matière :
] permettent de déterminer le champ de concentration cm sur la terrasse m.
Malheureusement, la géométrie du train de marches est a priori indéterminée. C'est un problème de frontière libre : la géométrie des marches détermine le champ de concentration sur les terrasses mais la dynamique de ces marches dépend elle-même du champ de concentration d'adatome à la surface 2.5.
Il nous faut donc une équation supplémentaire pour décrire la dynamique de la marche m. Elle nous est donnée par une équation de conservation de la matière au niveau de la marche m, qui traduit que l'avancée de celle-ci est proportionnelle au bilan des flux incidents de matière :