



suivant: Données expérimentales
monter: Échelles temporelles et spatiales
précédent: Échelles temporelles et spatiales
Table des matières
L'analyse de la relation de dispersion précédente pour un train de marches en phase nous apprend qu'il existe toute une bande de modes instables (voir fig.
[![[*]](crossref.gif) -b)]).
Ceux-ci s'étendent depuis q = 0, qui correspond au mode de Goldstone d'invariance par translation du système jusqu'à un mode de coupure de vecteur d'onde qc que nous définirons plus loin pour lequel tous les modes de vecteur d'onde supérieur sont stables.
Examinons le cas spécifique des grandes longueurs d'onde (
q
-b)]).
Ceux-ci s'étendent depuis q = 0, qui correspond au mode de Goldstone d'invariance par translation du système jusqu'à un mode de coupure de vecteur d'onde qc que nous définirons plus loin pour lequel tous les modes de vecteur d'onde supérieur sont stables.
Examinons le cas spécifique des grandes longueurs d'onde (
q
 1), pour les modes en phase (
1), pour les modes en phase (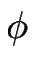 = 0) ; la relation de dispersion peut alors être développée (cf. éq. [
= 0) ; la relation de dispersion peut alors être développée (cf. éq. [![[*]](crossref.gif) ]).
La bande de modes instables (pour lesquels
]).
La bande de modes instables (pour lesquels
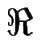 e(
e( ) > 0) est alors définie par 0 < q < qc (cf. fig. [
) > 0) est alors définie par 0 < q < qc (cf. fig. [![[*]](crossref.gif) -b)]), avec :
-b)]), avec :
où
fs = (d- - d+)/( + d+ + d-) est un paramètre qui rend compte de l'effet Ehrlich-Schwoebel.
Si
+ d+ + d-) est un paramètre qui rend compte de l'effet Ehrlich-Schwoebel.
Si  , définit par
, définit par
 = 2(qc
= 2(qc )2, est petit devant l'unité, le développement précédent de
)2, est petit devant l'unité, le développement précédent de
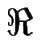 e(
e( ) est valable et seuls les modes de grande longueur d'onde (i.e de vecteur d'onde inférieure à qc) sont instables.
Pour
) est valable et seuls les modes de grande longueur d'onde (i.e de vecteur d'onde inférieure à qc) sont instables.
Pour
 = 0 tous les modes sont stables (seul le mode de Goldstone reste marginalement stable) ; le système est stable vis-à-vis d'une perturbation infinitésimale.
Le paramètre
= 0 tous les modes sont stables (seul le mode de Goldstone reste marginalement stable) ; le système est stable vis-à-vis d'une perturbation infinitésimale.
Le paramètre  , défini par
, défini par
 = = 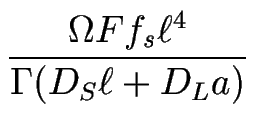 , ,
|
(3.21) |
mesure donc l'écart par rapport au seuil de l'instabilité.
C'est donc le petit paramètre
qui sera utilisé pour extraire la dynamique de l'évolution de la surface.
La petitesse de ce paramètre nous garantit la validité du régime de grande longueur d'onde.




suivant: Données expérimentales
monter: Échelles temporelles et spatiales
précédent: Échelles temporelles et spatiales
Table des matières
fred
2001-07-02
![[*]](crossref.gif) -b)]).
Ceux-ci s'étendent depuis q = 0, qui correspond au mode de Goldstone d'invariance par translation du système jusqu'à un mode de coupure de vecteur d'onde qc que nous définirons plus loin pour lequel tous les modes de vecteur d'onde supérieur sont stables.
Examinons le cas spécifique des grandes longueurs d'onde (
q
-b)]).
Ceux-ci s'étendent depuis q = 0, qui correspond au mode de Goldstone d'invariance par translation du système jusqu'à un mode de coupure de vecteur d'onde qc que nous définirons plus loin pour lequel tous les modes de vecteur d'onde supérieur sont stables.
Examinons le cas spécifique des grandes longueurs d'onde (
q![[*]](crossref.gif) ]).
La bande de modes instables (pour lesquels
]).
La bande de modes instables (pour lesquels
![[*]](crossref.gif) -b)]), avec :
-b)]), avec :
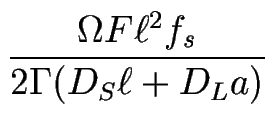
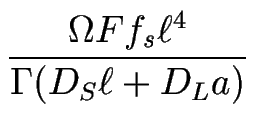 ,
,