



suivant: Analyse des échelles de
monter: MAIN
précédent: Solution stationnaire du train
Table des matières
Méandre des marches en l'absence de désorption
Intéressons nous
maintenant au problème de l'instabilité morphologique conduisant au méandre des marches.
Cette instabilité est analogue à celle de Mullins et Sekerka [#!Mullins64!#] : c'est-à-dire celle d'une interface en croissance dans un champ de diffusion.
Bales et Zangwill [#!Bales90!#] ont montré
qu'une surface vicinale en croissance par épitaxie se déstabilise en présence d'un effet Ehrlich-Schwoebel (
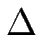
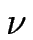 > 0) à la marche alors qu'un effet inverse3.1 stabilise cette dernière.
> 0) à la marche alors qu'un effet inverse3.1 stabilise cette dernière.
Les expériences de croissance MBE réalisées par Maroutian et al. sur le cuivre (1, 1, 17) [#!Maroutian99!#] montrent le développement d'une instabilité de méandre (cf. fig. [![[*]](crossref.gif) ]).
Elles sont réalisées à relativement faible température (
]).
Elles sont réalisées à relativement faible température (
 300 - 400K) et la désorption d'adatomes est extrêmement négligeable, les flux incidents utilisés sont eux aussi très faibles (
300 - 400K) et la désorption d'adatomes est extrêmement négligeable, les flux incidents utilisés sont eux aussi très faibles (
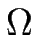 F
F  10-3s-1) et l'effet Ehrlich-Schwoebel aux marches semble être important.
C'est l'un des premiers systèmes sur lequel l'instabilité de méandre a pu être observée directement par STM.
10-3s-1) et l'effet Ehrlich-Schwoebel aux marches semble être important.
C'est l'un des premiers systèmes sur lequel l'instabilité de méandre a pu être observée directement par STM.
Les équations constitutives du modèle présentées au chapitre ![[*]](crossref.gif) se récrivent simplement.
La concentration d'adatomes cm sur la terrasse m (définie pour z compris entre zm et zm + 1 où zm est la position de la marche m) obéit à une équation de diffusion quasi statique :
se récrivent simplement.
La concentration d'adatomes cm sur la terrasse m (définie pour z compris entre zm et zm + 1 où zm est la position de la marche m) obéit à une équation de diffusion quasi statique :
D cm + F = 0 cm + F = 0
|
(3.1) |
La concentration est déterminée par deux conditions aux limites, une à chaque extrémité de la terrasse.
Ces conditions aux limites traduisent les cinétiques d'attachement des adatomes aux marches m et m + 1 et expriment la façon dont les flux d'adatomes arrivant aux marches sont reliés à l'écart à l'équilibre.
Proche de l'équilibre, elles s'écrivent sous une forme linéarisée « à la Onsager » :
D  . . cm( cm(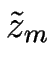 ) ) |
= |
  cm( cm(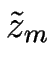 ) - ceqm ) - ceqm![$\displaystyle \left.\vphantom{ c_m({\tilde z}_m) - c_{eq_m} }\right]$](img138.gif) , , |
(3.2) |
D  . . cm( cm( ) ) |
= |
-   cm(zm + 1) - ceqm + 1 cm(zm + 1) - ceqm + 1![$\displaystyle \left.\vphantom{ c_m(z_{m+1}) - c_{eq_{m+1}} }\right]$](img70.gif) . . |
(3.3) |
zm est la position de la marche m dans un repère fixe (par exemple celui du laboratoire).
On définit 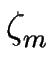 tel que
zm = m
tel que
zm = m +
+ 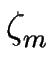 + V0t, où V0 est la vitesse stationnaire du train de marches droites et équidistantes.
+ V0t, où V0 est la vitesse stationnaire du train de marches droites et équidistantes.
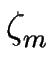 est donc la variation de position de la marche m, autour de sa configuration rectiligne dans un repère se déplaçant avec les marches.
Nous considérerons que le méandre des marches ne forme pas de « overhang » (c'est-à-dire que le méandre peut être représenté par une fonction univoque
est donc la variation de position de la marche m, autour de sa configuration rectiligne dans un repère se déplaçant avec les marches.
Nous considérerons que le méandre des marches ne forme pas de « overhang » (c'est-à-dire que le méandre peut être représenté par une fonction univoque 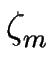 de x).
de x).
 est le vecteur unitaire normal à la marche et orienté dans le sens des z croissants.
est le vecteur unitaire normal à la marche et orienté dans le sens des z croissants.
 et
et  sont des coefficients cinétiques traduisant la facilité d'attachement des adatomes aux marches.
sont des coefficients cinétiques traduisant la facilité d'attachement des adatomes aux marches.  concerne les adatomes provenant de la terrasse inférieure et
concerne les adatomes provenant de la terrasse inférieure et  ceux venant de la terrasse supérieure.
Une cinétique instantanée se traduit par un coefficient cinétique infini alors qu'un attachement impossible correspond à un coefficient cinétique nul.
On introduit les longueurs cinétiques d'attachement ou longueurs Schwoebel : d+ et d- définies par
d± = D/
ceux venant de la terrasse supérieure.
Une cinétique instantanée se traduit par un coefficient cinétique infini alors qu'un attachement impossible correspond à un coefficient cinétique nul.
On introduit les longueurs cinétiques d'attachement ou longueurs Schwoebel : d+ et d- définies par
d± = D/ .
ceqm est la concentration d'équilibre local au voisinage de la marche m.
Elle est reliée par la relation de Gibbs-Thomson au potentiel chimique
.
ceqm est la concentration d'équilibre local au voisinage de la marche m.
Elle est reliée par la relation de Gibbs-Thomson au potentiel chimique  de la phase adsorbée en équilibre avec le solide [#!Bales90!#] :
de la phase adsorbée en équilibre avec le solide [#!Bales90!#] :
ceq = ceq0 e , ,
|
(3.4) |
où ceq0 est la concentration d'équilibre aux marches pour un train uniforme de marches droites. Proche de l'équilibre, la relation précédente peut se linéariser :
ceq = ceq0  1 + 1 +  + ... + ... . .
|
(3.5) |
Le potentiel chimique  est obtenu par dérivation fonctionnelle de l'énergie libre
est obtenu par dérivation fonctionnelle de l'énergie libre 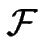 de configuration du train de marches :
où
de configuration du train de marches :
où
 =
= 

 dx, est le nombre de particules dans la phase solide.
De manière générale, cette énergie libre peut se décomposer en deux parties : l'une relative à la tension de ligne des marches, l'autre provenant de l'interaction élastique entre marches.
Cette interaction élastique n'intervenant dans le développement linéaire de l'instabilité que dans la stabilisation de la mise en paquets des marches et dans une renormalisation de la rigidité de ligne, nous la négligerons dans un premier temps.
Il s'en suit que le potentiel chimique
dx, est le nombre de particules dans la phase solide.
De manière générale, cette énergie libre peut se décomposer en deux parties : l'une relative à la tension de ligne des marches, l'autre provenant de l'interaction élastique entre marches.
Cette interaction élastique n'intervenant dans le développement linéaire de l'instabilité que dans la stabilisation de la mise en paquets des marches et dans une renormalisation de la rigidité de ligne, nous la négligerons dans un premier temps.
Il s'en suit que le potentiel chimique  est donné par la relation de Laplace [#!Mullins57!#] :
où
est donné par la relation de Laplace [#!Mullins57!#] :
où  est la courbure de la marche, définie par :
est la courbure de la marche, définie par :
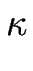 = - = -  , ,
|
(3.8) |
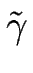 est la rigidité de ligne de la marche et
est la rigidité de ligne de la marche et 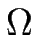 l'aire atomique dans la phase solide.
l'aire atomique dans la phase solide.
La dernière équation du modèle est une équation de continuité traduisant la conservation de la matière au niveau de la marche m.
La vitesse de la marche m est simplement proportionnelle au bilan des flux atomiques incidents :
Vm =   D D 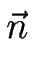 . . cm(zm) - D cm(zm) - D 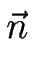 . . cm - 1(zm) cm - 1(zm)![$\displaystyle \left.\vphantom{ D \; \vec{n}.\vec{\nabla} c_m(z_m) - D \; \vec{n}.\vec{\nabla}c_{m-1}(z_m) }\right]$](img163.gif) + a + a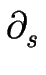  DL DL 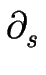  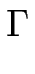   ![$\displaystyle \left.\vphantom{ D_L \; \partial_s \left( \Gamma \kappa_m \right) }\right]$](img167.gif) . .
|
(3.9) |
Le premier terme du membre de droite représente le bilan du flux atomique provenant de la diffusion sur les terrasses adjacentes à la marche.
Le second exprime l'apport de matière dû aux atomes déjà attachés à la marche et diffusant le long de celle-ci ; on parlera de diffusion de ligne.
Cette expression est en accord avec celle de Mullins [#!Mullins57!#]. La constante de diffusion macroscopique le long de la marche est définie par la relation d'Einstein comme :
DL = a Dst cst, où Dst et cst sont respectivement la constante de diffusion et la concentration d'atomes mobiles le long de la marche.
Cependant, cst n'est pas bien définie le long des marches.
On peut alors utiliser une expression plus générale dérivée de la formule de Kubo [#!Villain95!#,#!Giesen-Seibert93!#] :
DL = a2/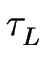 où
où 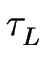 est le temps caractéristique de détachement d'un atome depuis un cran 3.2 (voir figure [
est le temps caractéristique de détachement d'un atome depuis un cran 3.2 (voir figure [![[*]](crossref.gif) ]).
]).
Figure:
Schéma d'une marche cristalline à l'échelle atomique : son profil est rugueux et présente de nombreux crans.
|
|
La configuration de la surface qui nous servira de base est l'état stationnaire où les marches sont droites et équidistantes, avançant toutes à la même vitesse constante V0.
La désorption des adatomes de la surface étant négligeable, il y a conservation globale de la matière : en régime stationnaire, tous les atomes arrivant sur les terrasses sont « capturés » par les marches.
Le nombre d'atomes arrivant sur une terrasse de largeur  et de longueur L est
F
et de longueur L est
F L par unité de temps.
Le nombre d'atomes capturés par une marche avançant à la vitesse V0 est
V0 L/
L par unité de temps.
Le nombre d'atomes capturés par une marche avançant à la vitesse V0 est
V0 L/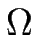 par unité de temps.
Le bilan résultant de la conservation globale de la matière impose l'égalité de ces deux nombres soit :
par unité de temps.
Le bilan résultant de la conservation globale de la matière impose l'égalité de ces deux nombres soit :
V0 =  F F 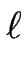
|
(3.10) |
Dans un système physique, la surface vicinale n'est jamais parfaitement régulière : les marches ne sont ni parfaitement droites ni régulièrement réparties.
Il y a à cela deux raisons principales : d'une part l'imperfection du clivage et d'autre part les fluctuations statistiques importantes pour les objets unidimensionnels que sont les marches [#!Pierre-Louis97!#]. Nous négligeons dans ce travail les fluctuations d'origine statistique pour nous concentrer sur les origines déterministes de l'instabilité de méandre.
La première étape consiste donc à étudier la stabilité du train uniforme de marches droites vis-à-vis d'une perturbation infinitésimale.
La perturbation étant supposée faible, on étudiera tout d'abord la réponse linéaire du système à cette dernière.
La perturbation du train de marches
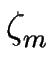 (x, t) peut se décomposer sur une base de Fourier :
(x, t) peut se décomposer sur une base de Fourier :
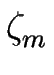 (x, t) = (x, t) =     e e t + im t + im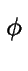 + iqx d + iqx d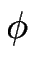 dq d dq d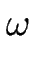 , ,
|
(3.11) |
où
 est par définition la transformée de Fourier de
est par définition la transformée de Fourier de
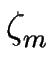 (x, t).
Les différents modes de Fourier ne se couplant pas dans une analyse linéaire, on étudiera la réponse
(x, t).
Les différents modes de Fourier ne se couplant pas dans une analyse linéaire, on étudiera la réponse  du système à un seul mode de Fourier (
du système à un seul mode de Fourier (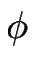 , q).
La perturbation prend la forme :
, q).
La perturbation prend la forme :
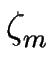 (x, t) =
(x, t) = 
 e
e t + im
t + im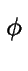 + iqx.
Les équations constitutives [
+ iqx.
Les équations constitutives [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] du modèle sont résolues en développant à l'ordre le plus bas la concentration par rapport à la perturbation
] du modèle sont résolues en développant à l'ordre le plus bas la concentration par rapport à la perturbation 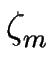 :
cm = cm0 +
:
cm = cm0 + 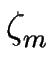 cm1, où cm1 est la réponse du champ de concentration à la perturbation.
cm1, où cm1 est la réponse du champ de concentration à la perturbation.
Le détail des calculs est donné en annexe ![[*]](crossref.gif) et aboutit à la relation de dispersion suivante :
et aboutit à la relation de dispersion suivante :
| |
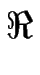 e( e(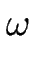 ) ) |
= - 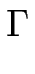 q2 q2 DS DS   2 2 ch(q ch(q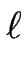 ) - cos( ) - cos(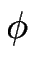 ) ) + q(d+ + d-) sh(q + q(d+ + d-) sh(q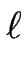 ) ) + a DLq2 + a DLq2![$\displaystyle \left.\vphantom{ D_S \, \frac{q}{{\cal D}} \left( 2 \left({\rm ch...
...(\phi) \right) + q(d_++d_-) \; {\rm sh}(q \ell) \right) + a \, D_L q^2 }\right]$](img187.gif) |
|
| + |
 F F |
     (d- + d+) (d- + d+) q q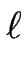 sh(q sh(q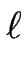 ) - ch(q ) - ch(q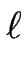 ) + cos( ) + cos(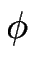 ) ) + +  q q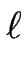 sh(q sh(q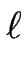 ) )![$\displaystyle \left.\vphantom{ (d_-+d_+) \left( q \ell \; {\rm sh}(q \ell) - {\...
...ell) + \cos (\phi) \right) + \frac{\ell}{2} q \ell \; {\rm sh}(q \ell) }\right]$](img196.gif) , , |
|
| |
|
|
(3.12) |
où  est donné par :
est donné par :
 = (d+ + d-) q ch(q = (d+ + d-) q ch(q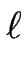 ) + (d+d- q2 + 1) sh(q ) + (d+d- q2 + 1) sh(q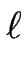 ) , ) ,
|
(3.13) |
et 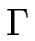 est une longueur caractérisant les effets de tension de ligne, reliée à la tension de ligne
est une longueur caractérisant les effets de tension de ligne, reliée à la tension de ligne
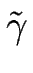 par :
par :
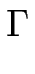 = =  . .
|
(3.14) |
Seuls les coefficients de diffusion macroscopiques sur les terrasses
DS = D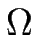 ceq0 et le long des marches DL entrent en compte dans cette relation.
Le coefficient de diffusion D des adatomes sur les terrasses n'apparaît jamais seul.
ceq0 et le long des marches DL entrent en compte dans cette relation.
Le coefficient de diffusion D des adatomes sur les terrasses n'apparaît jamais seul.
Figure:
Relation de dispersion.
![\includegraphics[width=6.5cm,angle=0]{../Images/im_wr_2.eps}](img199.gif) |
![\includegraphics[width=6.5cm,angle=0]{../Images/wr_q.eps}](img200.gif) |
a)Taux de croissance
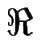 e( e( ) en fonction du déphasage ) en fonction du déphasage 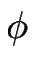 et du vecteur d'onde q. Les modes instables correspondent à et du vecteur d'onde q. Les modes instables correspondent à
 e( e( ) > 0 et sont représentés en blanc. À q fixé, les modes les plus instables se produisent à déphasage ) > 0 et sont représentés en blanc. À q fixé, les modes les plus instables se produisent à déphasage 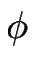 nul. Le mode le plus instable est noté M. nul. Le mode le plus instable est noté M. |
b)Taux de croissance à déphasage 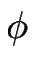 nul. Il existe toute une bande de modes instables pour 0 < q < qc. On note qm, le vecteur d'onde du mode le plus instable M. nul. Il existe toute une bande de modes instables pour 0 < q < qc. On note qm, le vecteur d'onde du mode le plus instable M. |
|
Lorsque
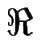 e(
e( ) est négative, le train de marches est stable vis-à-vis de la perturbation à laquelle elle est soumise : cette dernière s'atténue jusqu'à disparaître.
Une instabilité est signalée par une valeur positive de la partie réelle de
) est négative, le train de marches est stable vis-à-vis de la perturbation à laquelle elle est soumise : cette dernière s'atténue jusqu'à disparaître.
Une instabilité est signalée par une valeur positive de la partie réelle de  .
Nous définissons de façon générale le seuil de l'instabilité comme la valeur critique d'un paramètre de contrôle réalisant l'annulation du taux de croissance
.
Nous définissons de façon générale le seuil de l'instabilité comme la valeur critique d'un paramètre de contrôle réalisant l'annulation du taux de croissance  .
En deçà de ce seuil, le système est stable vis-à-vis d'une perturbation infinitésimale alors qu'il est instable au-delà du seuil.
Dans le cas présent, notre paramètre de contrôle est le flux incident F.
En présence d'effet Ehrlich-Schwoebel (
.
En deçà de ce seuil, le système est stable vis-à-vis d'une perturbation infinitésimale alors qu'il est instable au-delà du seuil.
Dans le cas présent, notre paramètre de contrôle est le flux incident F.
En présence d'effet Ehrlich-Schwoebel (
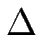
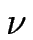 > 0, soit d- > d+), le train de marche est instable en croissance, pour un flux F aussi faible soit-il. Le seuil de l'instabilité correspond à F = 0.
L'examen de la relation de dispersion nous apprend de plus que le mode le plus instable (i.e. celui dont le taux de croissance
> 0, soit d- > d+), le train de marche est instable en croissance, pour un flux F aussi faible soit-il. Le seuil de l'instabilité correspond à F = 0.
L'examen de la relation de dispersion nous apprend de plus que le mode le plus instable (i.e. celui dont le taux de croissance 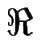 e(w) est le plus important) est un mode en phase (
e(w) est le plus important) est un mode en phase (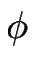 = 0) (voir figure [
= 0) (voir figure [![[*]](crossref.gif) -a)]). Pour ce mode, le taux de croissance prend la forme (pour F petit, on néglige les termes en F q4) :
-a)]). Pour ce mode, le taux de croissance prend la forme (pour F petit, on néglige les termes en F q4) :
Re[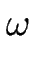 (q (q  1, 1,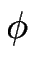 = 0)] = = 0)] =  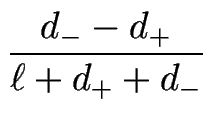 q2 - (DS q2 - (DS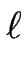 + DLa) + DLa)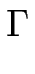 q4 . q4 .
|
(3.15) |
La partie imaginaire de  traduit quant à elle, les effets propagatifs de l'instabilité :
traduit quant à elle, les effets propagatifs de l'instabilité :
 m( m(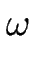 ) = ) =  F sin( F sin(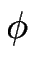 ) ) ( (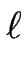 + d+ + d-). + d+ + d-).
|
(3.16) |
Dans la limite des marches droites (q = 0), nous avons
 m(
m( ) =
) = 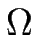 F sin(
F sin(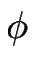 ). Il s'en suit que la solution perturbée prend la forme
:
). Il s'en suit que la solution perturbée prend la forme
:
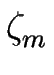 (t) (t) 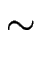 ei ei F t sin( F t sin(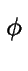 ) + im ) + im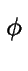 = ei = ei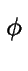 / /  m m + tV0sin( + tV0sin(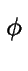 )/ )/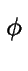 ![$\scriptstyle \left.\vphantom{ m\ell + t V_0 \sin(\phi)/\phi }\right]$](img211.gif) . .
|
(3.17) |
Nous avons ici introduit la vitesse du train uniforme de marches
V0 = 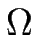 F
F .
On a alors :
.
On a alors :
 (t + dt) = (t + dt) = 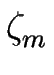 (t) ei (t) ei   m m  - V dt - V dt![$\scriptstyle \left.\vphantom{ \Delta m \; \ell - V \, dt }\right]$](img216.gif) , ,
|
(3.18) |
où
V = - V0 sin(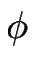 )/
)/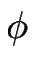 = - V0 sinc(
= - V0 sinc(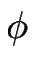 ).
La perturbation franchit une distance
-
).
La perturbation franchit une distance
- 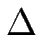 m
m  en un temps donné par
dt = -
en un temps donné par
dt = - 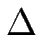 m
m  /V.
Cela signifie que dans le référentiel mobile se déplaçant à la vitesse constante V0 du train uniforme de marches, la perturbation se déplace à une vitesse donnée par3.3 :
/V.
Cela signifie que dans le référentiel mobile se déplaçant à la vitesse constante V0 du train uniforme de marches, la perturbation se déplace à une vitesse donnée par3.3 :
V = - V0 sinc(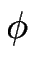 ) . ) .
|
(3.19) |
Les modes proches du mode en phase (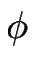 = 0) sont donc advectés vers l'arrière.
= 0) sont donc advectés vers l'arrière.
Sous-sections




suivant: Analyse des échelles de
monter: MAIN
précédent: Solution stationnaire du train
Table des matières
fred
2001-07-02
![]()
![]() > 0) à la marche alors qu'un effet inverse3.1 stabilise cette dernière.
> 0) à la marche alors qu'un effet inverse3.1 stabilise cette dernière.
![[*]](crossref.gif) ]).
Elles sont réalisées à relativement faible température (
]).
Elles sont réalisées à relativement faible température (
![]() 300 - 400K) et la désorption d'adatomes est extrêmement négligeable, les flux incidents utilisés sont eux aussi très faibles (
300 - 400K) et la désorption d'adatomes est extrêmement négligeable, les flux incidents utilisés sont eux aussi très faibles (
![]() F
F ![]() 10-3s-1) et l'effet Ehrlich-Schwoebel aux marches semble être important.
C'est l'un des premiers systèmes sur lequel l'instabilité de méandre a pu être observée directement par STM.
10-3s-1) et l'effet Ehrlich-Schwoebel aux marches semble être important.
C'est l'un des premiers systèmes sur lequel l'instabilité de méandre a pu être observée directement par STM.
![[*]](crossref.gif) se récrivent simplement.
La concentration d'adatomes cm sur la terrasse m (définie pour z compris entre zm et zm + 1 où zm est la position de la marche m) obéit à une équation de diffusion quasi statique :
se récrivent simplement.
La concentration d'adatomes cm sur la terrasse m (définie pour z compris entre zm et zm + 1 où zm est la position de la marche m) obéit à une équation de diffusion quasi statique :
 ,
,
![[*]](crossref.gif) ]).
]).
![\includegraphics[width=10cm,angle=0]{../Images/kink.eps}](img169.gif)
![]() (x, t) peut se décomposer sur une base de Fourier :
(x, t) peut se décomposer sur une base de Fourier :



![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] du modèle sont résolues en développant à l'ordre le plus bas la concentration par rapport à la perturbation
] du modèle sont résolues en développant à l'ordre le plus bas la concentration par rapport à la perturbation ![[*]](crossref.gif) et aboutit à la relation de dispersion suivante :
et aboutit à la relation de dispersion suivante :

![[*]](crossref.gif) -a)]). Pour ce mode, le taux de croissance prend la forme (pour F petit, on néglige les termes en F q4) :
-a)]). Pour ce mode, le taux de croissance prend la forme (pour F petit, on néglige les termes en F q4) :
![]() traduit quant à elle, les effets propagatifs de l'instabilité :
traduit quant à elle, les effets propagatifs de l'instabilité :