



suivant: Résultats numériques
monter: Méandre des marches en
précédent: Méandre des marches en
Table des matières
Plaçons-nous tout d'abord dans la limite unilatérale
; ce qui correspond à un attachement instantané des adatomes aux marches depuis la terrasse inférieure et à un attachement impossible depuis la terrasse supérieure :

 +
+ 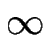 ;
; = 0 (ou, en terme de longueur Schwoebel, d+ = 0 et
d-
= 0 (ou, en terme de longueur Schwoebel, d+ = 0 et
d-  +
+ 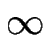 ). Cela constitue une bonne approximation des conditions expérimentales de croissance de
Cu(1, 1, 17) réalisées par Maroutian et al.
Dans cette limite, les relations cinétiques [
). Cela constitue une bonne approximation des conditions expérimentales de croissance de
Cu(1, 1, 17) réalisées par Maroutian et al.
Dans cette limite, les relations cinétiques [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] se récrivent simplement :
] se récrivent simplement :
cm(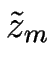 ) ) |
= |
ceqm , |
(3.58) |
 . .  cm( cm( ) ) |
= |
0 . |
(3.59) |
Le détail des calculs est laissé en annexe ![[*]](crossref.gif) et conduit, à l'ordre dominant à l'équation d'évolution suivante pour le méandre en phase :
et conduit, à l'ordre dominant à l'équation d'évolution suivante pour le méandre en phase :
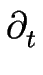  = - = -     - -  DS DS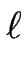 + DLa(1 + ( + DLa(1 + (  )2)1/2 )2)1/2  ![$\displaystyle \left.\vphantom{
\frac{\Omega F\ell^2}{2} \frac{\partial_x \zeta...
...2} \right)
\frac{\partial_x (\Gamma \kappa)}{(1+(\partial_x\zeta)^2)} }\right]$](img327.gif) , ,
|
(3.60) |
où 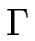 est une longueur caractérisant les effets de tension de ligne et reliée à la tension de ligne
est une longueur caractérisant les effets de tension de ligne et reliée à la tension de ligne
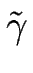 par :
par :
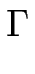 = =  . .
|
(3.61) |
Mis à part le terme proportionnel à DL qui tient compte de la diffusion de ligne, nous retrouvons l'équation dérivée précédemment par Pierre-Louis et al. [#!Pierre-Louis98a!#].
En introduisant la mobilité macroscopique  et le potentiel chimique
et le potentiel chimique
 =
= 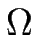
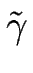
 = kB T
= kB T 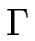
 ,
cette équation peut se récrire sous une forme plus compacte :
,
cette équation peut se récrire sous une forme plus compacte :
où s est l'abscisse curviligne le long de la marche et
 =
=  /[1 + (
/[1 + (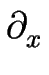
 )2]1/2
est la distance entre deux marches mesurée le long de leur normale commune
(voir Fig. [
)2]1/2
est la distance entre deux marches mesurée le long de leur normale commune
(voir Fig. [![[*]](crossref.gif) ] pour les définitions géométriques).
La mobilité effective s'écrit :
] pour les définitions géométriques).
La mobilité effective s'écrit :
 = =  . .
|
(3.63) |
La décomposition de la vitesse des marches en parties déstabilisante et stabilisante, démontrée précédemment est clairement visible sur l'équation [![[*]](crossref.gif) ].
Le premier terme du membre de droite de l'équation [
].
Le premier terme du membre de droite de l'équation [![[*]](crossref.gif) ] représente la contribution déstabilisante de la dynamique. Il provient de la collecte d'adatomes par la marche et peut se retrouver par un simple calcul géométrique.
Considérons un élément de marche de longueur ds et appelons
] représente la contribution déstabilisante de la dynamique. Il provient de la collecte d'adatomes par la marche et peut se retrouver par un simple calcul géométrique.
Considérons un élément de marche de longueur ds et appelons 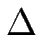 S, l'élément de surface de la terrasse faisant front à l'élément de marche ds (voir fig. [
S, l'élément de surface de la terrasse faisant front à l'élément de marche ds (voir fig. [![[*]](crossref.gif) -a]).
Si l'élément de marche ds se déplace avec une vitesse normale vn, alors il capture
vn ds/
-a]).
Si l'élément de marche ds se déplace avec une vitesse normale vn, alors il capture
vn ds/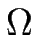 adatomes par unité de temps.
Le flux incident F amène quant à lui
F
adatomes par unité de temps.
Le flux incident F amène quant à lui
F 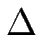 S atomes par unité de temps sur la surface
S atomes par unité de temps sur la surface 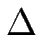 S.
S.
Figure:
Illustration géométrique de l'origine du terme déstabilisant.
|
|
La loi de conservation de la matière pour cet élément de surface s'écrit :
 = F = F S + j || (s) - j || (s + S + j || (s) - j || (s +  s) , s) ,
|
(3.64) |
où
j || est un flux de matière sur la terrasse, parallèle aux marches.
Appelons A(s) l'aire cumulée de terrasse devant la marche telle que
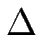 S = A(s + ds) - A(s) :
S = A(s + ds) - A(s) :
A(s) =  dA . dA .
|
(3.65) |
Alors l'aire différentielle dA s'écrit :
| dA |
= |
   ds + ds +    d d |
|
| |
= |
    + +     ![$\displaystyle \left.\vphantom{ \left( \frac{\partial A}{\partial s} \right)_{\t...
...eft( \frac{\partial A}{\partial \theta} \right)_{s} \frac{d\theta}{ds} }\right]$](img347.gif) ds ds |
|
| |
= |
 dA dA + +  dA dA . . |
(3.66) |
Le premier terme relate les variations de A lorsqu'on se déplace le long des marches
en supposant celles-ci localement rectilignes ( fixé) tandis que le second
tient compte des variations de courbure (
fixé) tandis que le second
tient compte des variations de courbure (
 = d
= d /ds) le long des
marches.
À
/ds) le long des
marches.
À  fixé, dA est simplement proportionnel à la largeur locale de la
terrasse
fixé, dA est simplement proportionnel à la largeur locale de la
terrasse
 soit :
L'aire algébrique hachurée sur la figure [
soit :
L'aire algébrique hachurée sur la figure [![[*]](crossref.gif) -b] s'écrit :
1/2×
-b] s'écrit :
1/2×
 sin(
sin( ), ce qui permet de déterminer la variation d'aire due à la courbure :
), ce qui permet de déterminer la variation d'aire due à la courbure :
 dA dA |
= |
d   cos( cos( ) sin( ) sin( ) )![$\displaystyle \left.\vphantom{ \frac{1}{2} \ell^2 \cos(\theta) \; \sin(\theta) }\right]$](img355.gif) , , |
(3.68) |
| |
= |
    cos( cos( ) sin( ) sin( ) )![$\displaystyle \left.\vphantom{ \frac{1}{2} \ell^2 \cos(\theta) \; \sin(\theta) }\right]$](img355.gif) ds , ds , |
(3.69) |
Soit pour l'aire différentielle dA :
dA =  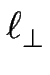 + +     cos( cos( )sin( )sin( ) ) ![$\displaystyle \left.\vphantom{ \ell_\perp
+ \frac{\partial}{\partial s} \left( \frac{1}{2} \ell^2 \cos(\theta) \sin(\theta) \right)
}\right]$](img360.gif) ds ds
|
(3.70) |
La contribution au bilan de masse du flux de matière
j || est négligeable devant celle due au flux incident F. En effet, le flux
j || ne peut provenir que d'une variation de la géométrie locale de la terrasse le long de la marche.
Or localement, la terrasse est complètement décrite par sa largeur
 d'où :
Ce qui, compte tenu de l'échelle du méandre est négligeable devant la contribution donnée par
d'où :
Ce qui, compte tenu de l'échelle du méandre est négligeable devant la contribution donnée par
 S
S  A
A 
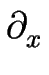
 , d'où :
, d'où :
 = F = F  dA dA
|
(3.72) |
À l'ordre dominant, en prenant la limite
ds  0 on obtient alors pour la vitesse normale :
0 on obtient alors pour la vitesse normale :
| vn |
= |
 F F  , , |
|
| |
= |
 F F 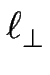 + +     cos( cos( )sin( )sin( ) ) ![$\displaystyle \left.\vphantom{ \ell_\perp + \frac{\partial}{\partial_s} \left( \frac{1}{2} \ell^2 \cos(\theta) \sin(\theta) \right) }\right]$](img366.gif) . . |
(3.73) |
En retranchant la vitesse moyenne
< vn > = 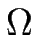 F
F de la marche,
on retrouve le terme déstabilisant de l'équation du méandre :
de la marche,
on retrouve le terme déstabilisant de l'équation du méandre :
vn -  F F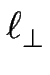 |
= |
   cos( cos( )sin( )sin( ) ) |
|
| |
= |
   tan( tan( ) ) ; ; |
(3.74) |
soit, en coordonnées cartésiennes 3.6:
Comme le calcul géométrique le montre, le terme déstabilisant est directement lié à la courbure
 = d
= d /ds de la marche.
En effet, on a :
/ds de la marche.
En effet, on a :
vn -  F F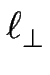 |
= |
   cos( cos( )sin( )sin( ) ) |
|
| |
= |
   sin(2 sin(2 ) )  , , |
|
| |
= |
 F F 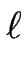   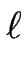 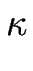  . . |
(3.76) |
Le second terme de l'équation [![[*]](crossref.gif) ] :
] :
représente la partie relaxante de la dynamique ; c'est tout simplement le terme de relaxation de Cahn-Hilliard [#!Cahn58!#] [#!Mullins57!#] avec cependant ici, une mobilité  dépendant de l'orientation locale de la marche.
Il décrit les effets thermodynamiques contribuant à ramener le système vers sa configuration d'équilibre où les marches sont droites et équidistantes.
Dans le cas présent, pour un train de marches en phase, les marches sont déjà équidistantes et c'est la tension de ligne qui est responsable de la relaxation du méandre vers un profil de marche droit. Cette tension de ligne modifie le potentiel chimique aux marches ce qui à pour effet d'induire un flux de matière.
Cette relaxation peut s'opérer à travers deux processus que nous avons inclus ici.
Le premier correspond à un détachement des adatomes des marches qui se rattachent ailleurs après avoir diffusé sur les terrasses.
Le second processus et qui semble être celui dominant dans le cas du
Cu(1, 1, 17) [#!Maroutian99!#] opère par diffusion des adatomes le long de la marche, on parle de diffusion de ligne.
Dans le cas où les marches ne seraient plus en phase, un autre processus de relaxation
qui aurait comme effet de rendre le train de marches uniforme, interviendrait.
Il est dû à une répulsion entre marches induite d'une part par le champ de diffusion (répulsion diffusive) et d'autre part et de façon encore plus importante par une répulsion d'origine élastique.
En effet les marches constituent des défauts à la surface et affectent le champ élastique ; il en résulte, dans le cas de l'homoépitaxie, une répulsion effective en 1/
dépendant de l'orientation locale de la marche.
Il décrit les effets thermodynamiques contribuant à ramener le système vers sa configuration d'équilibre où les marches sont droites et équidistantes.
Dans le cas présent, pour un train de marches en phase, les marches sont déjà équidistantes et c'est la tension de ligne qui est responsable de la relaxation du méandre vers un profil de marche droit. Cette tension de ligne modifie le potentiel chimique aux marches ce qui à pour effet d'induire un flux de matière.
Cette relaxation peut s'opérer à travers deux processus que nous avons inclus ici.
Le premier correspond à un détachement des adatomes des marches qui se rattachent ailleurs après avoir diffusé sur les terrasses.
Le second processus et qui semble être celui dominant dans le cas du
Cu(1, 1, 17) [#!Maroutian99!#] opère par diffusion des adatomes le long de la marche, on parle de diffusion de ligne.
Dans le cas où les marches ne seraient plus en phase, un autre processus de relaxation
qui aurait comme effet de rendre le train de marches uniforme, interviendrait.
Il est dû à une répulsion entre marches induite d'une part par le champ de diffusion (répulsion diffusive) et d'autre part et de façon encore plus importante par une répulsion d'origine élastique.
En effet les marches constituent des défauts à la surface et affectent le champ élastique ; il en résulte, dans le cas de l'homoépitaxie, une répulsion effective en 1/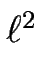 où
où  est la distance entre marches. La prise en compte des effets élastiques sera abordée ultérieurement.
est la distance entre marches. La prise en compte des effets élastiques sera abordée ultérieurement.
L'équation d'évolution du méandre [![[*]](crossref.gif) ] peut se récrire en
utilisant un système de coordonnées dites « intrinsèques ».
Le méandre est alors décrit en terme d'angle
] peut se récrire en
utilisant un système de coordonnées dites « intrinsèques ».
Le méandre est alors décrit en terme d'angle  entre la normale aux marches et une
direction fixée (ici la direction de la vicinalité z) et paramétrisé par l'abscisse
curviligne s (qui rend unitaire la métrique).
La description de ces coordonnées appliquées au méandre est donnée sur la figure [
entre la normale aux marches et une
direction fixée (ici la direction de la vicinalité z) et paramétrisé par l'abscisse
curviligne s (qui rend unitaire la métrique).
La description de ces coordonnées appliquées au méandre est donnée sur la figure [![[*]](crossref.gif) ].
].
Figure:
Définitions géométriques des coordonnées dites « intrinsèques ». s est l'abscisse curviligne le long des marches et  est un angle polaire entre une direction fixée (ici z) et la normale à la marche.
À cause du comportement d'échelle du méandre, les marches sont localement parallèles et la distance entre marches est localement donnée par
est un angle polaire entre une direction fixée (ici z) et la normale à la marche.
À cause du comportement d'échelle du méandre, les marches sont localement parallèles et la distance entre marches est localement donnée par
 , la distance évaluée le long de leur normale commune.
, la distance évaluée le long de leur normale commune.
|
|
L'équation d'évolution [![[*]](crossref.gif) ] prend alors la forme suivante :
] prend alors la forme suivante :
vn = 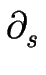   tan( tan( ) + ) +  DS DS 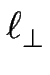 + DL a + DL a 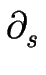  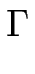 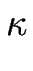  ![$\displaystyle \left.\vphantom{ \frac{\Omega \, F \, \ell_\perp^2}{2} \tan(\thet...
...erp + D_L \, a \right) \, \partial_{s} \left( \Gamma \, \kappa \right) }\right]$](img390.gif) . .
|
(3.78) |
Sous-sections




suivant: Résultats numériques
monter: Méandre des marches en
précédent: Méandre des marches en
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] se récrivent simplement :
] se récrivent simplement :
![]()
![]() +
+ ![]() ;
;![]() = 0 (ou, en terme de longueur Schwoebel, d+ = 0 et
d-
= 0 (ou, en terme de longueur Schwoebel, d+ = 0 et
d- ![]() +
+ ![]() ). Cela constitue une bonne approximation des conditions expérimentales de croissance de
Cu(1, 1, 17) réalisées par Maroutian et al.
Dans cette limite, les relations cinétiques [
). Cela constitue une bonne approximation des conditions expérimentales de croissance de
Cu(1, 1, 17) réalisées par Maroutian et al.
Dans cette limite, les relations cinétiques [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] se récrivent simplement :
] se récrivent simplement :
![[*]](crossref.gif) et conduit, à l'ordre dominant à l'équation d'évolution suivante pour le méandre en phase :
où
et conduit, à l'ordre dominant à l'équation d'évolution suivante pour le méandre en phase :
où ![]() et le potentiel chimique
et le potentiel chimique
![]() =
= ![]()
![]()
![]() = kB T
= kB T ![]()
![]() ,
cette équation peut se récrire sous une forme plus compacte :
,
cette équation peut se récrire sous une forme plus compacte :
![[*]](crossref.gif) ] pour les définitions géométriques).
La mobilité effective s'écrit :
La décomposition de la vitesse des marches en parties déstabilisante et stabilisante, démontrée précédemment est clairement visible sur l'équation [
] pour les définitions géométriques).
La mobilité effective s'écrit :
La décomposition de la vitesse des marches en parties déstabilisante et stabilisante, démontrée précédemment est clairement visible sur l'équation [![[*]](crossref.gif) ].
Le premier terme du membre de droite de l'équation [
].
Le premier terme du membre de droite de l'équation [![[*]](crossref.gif) ] représente la contribution déstabilisante de la dynamique. Il provient de la collecte d'adatomes par la marche et peut se retrouver par un simple calcul géométrique.
Considérons un élément de marche de longueur ds et appelons
] représente la contribution déstabilisante de la dynamique. Il provient de la collecte d'adatomes par la marche et peut se retrouver par un simple calcul géométrique.
Considérons un élément de marche de longueur ds et appelons ![[*]](crossref.gif) -a]).
Si l'élément de marche ds se déplace avec une vitesse normale vn, alors il capture
vn ds/
-a]).
Si l'élément de marche ds se déplace avec une vitesse normale vn, alors il capture
vn ds/![]() S = A(s + ds) - A(s) :
S = A(s + ds) - A(s) :
![[*]](crossref.gif) -b] s'écrit :
1/2×
-b] s'écrit :
1/2× = F
= F  dA
dA
 cos(
cos( tan(
tan(
 cos(
cos( sin(2
sin(2
![[*]](crossref.gif) ] :
] :
![[*]](crossref.gif) ] peut se récrire en
utilisant un système de coordonnées dites « intrinsèques ».
Le méandre est alors décrit en terme d'angle
] peut se récrire en
utilisant un système de coordonnées dites « intrinsèques ».
Le méandre est alors décrit en terme d'angle ![]() entre la normale aux marches et une
direction fixée (ici la direction de la vicinalité z) et paramétrisé par l'abscisse
curviligne s (qui rend unitaire la métrique).
La description de ces coordonnées appliquées au méandre est donnée sur la figure [
entre la normale aux marches et une
direction fixée (ici la direction de la vicinalité z) et paramétrisé par l'abscisse
curviligne s (qui rend unitaire la métrique).
La description de ces coordonnées appliquées au méandre est donnée sur la figure [![[*]](crossref.gif) ].
].
![\includegraphics[width=10cm,angle=0]{../Images/coord_intrins.eps}](img383.gif)
![[*]](crossref.gif) ] prend alors la forme suivante :
] prend alors la forme suivante :