![[*]](crossref.gif) ], en l'absence de diffusion de ligne a été dérivée par Pierre-Louis et al. [#!Pierre-Louis98a!#].
Les auteurs l'ont simulée en utilisant un schéma numérique simple.
Les principaux résultats trouvés sont les suivants :
], en l'absence de diffusion de ligne a été dérivée par Pierre-Louis et al. [#!Pierre-Louis98a!#].
Les auteurs l'ont simulée en utilisant un schéma numérique simple.
Les principaux résultats trouvés sont les suivants :
L'équation du méandre [![[*]](crossref.gif) ], en l'absence de diffusion de ligne a été dérivée par Pierre-Louis et al. [#!Pierre-Louis98a!#].
Les auteurs l'ont simulée en utilisant un schéma numérique simple.
Les principaux résultats trouvés sont les suivants :
], en l'absence de diffusion de ligne a été dérivée par Pierre-Louis et al. [#!Pierre-Louis98a!#].
Les auteurs l'ont simulée en utilisant un schéma numérique simple.
Les principaux résultats trouvés sont les suivants :
Ces singularités apparaissant à temps fini posent problème.
Aux pointes, la courbure devient infinie et le méandre, en tant que système physique thermodynamique n'a aucun intérêt à laisser se développer une telle structure.
Une inspection plus précise des résultats numériques précédents [#!Pierre-Louis98a!#] nous a permis de conclure à une déficience numérique dans l'évaluation des termes stabilisants de l'équation du méandre.
Ce sont en effets ces mêmes termes qui interdisent l'apparition de singularités à temps fini.
Un examen spectral du méandre nous a montré que la dynamique laisse se développer au cours du temps des modes de fréquences de plus en plus élevées.
Une intégration numérique inappropriée conduit alors à une amplification du bruit numérique.
Il nous a paru alors opportun d'améliorer le schéma numérique utilisé.
Le schéma numérique « Euler explicite » utilisé précédemment par Pierre-Louis et al. [#!Pierre-Louis98a!#] a été remplacé par un schéma plus stable.
Le schéma retenu est un schéma BDF (« backward differentiation formulae », voir annexe ![[*]](crossref.gif) ) qui est connu pour sa L-stabilité ; c'est-à-dire qu'en plus d'être inconditionnellement stable, il atténue de façon optimum les hautes fréquences correspondant à du bruit numérique.
) qui est connu pour sa L-stabilité ; c'est-à-dire qu'en plus d'être inconditionnellement stable, il atténue de façon optimum les hautes fréquences correspondant à du bruit numérique.
Afin d'évaluer correctement les variations spatiales du méandre, nous allons simplifier la formulation de l'équation d'évolution dynamique en utilisant les propriétés d'invariance par translation et de conservation du système.
À cause de la propriété d'invariance par translation, l'équation de la dynamique ne fait pas intervenir la valeur du méandre ![]() mais uniquement ses dérivées.
De plus, comme la dynamique est celle d'un système conservé, l'équation de la dynamique s'écrit comme la divergence d'un flux :
mais uniquement ses dérivées.
De plus, comme la dynamique est celle d'un système conservé, l'équation de la dynamique s'écrit comme la divergence d'un flux :
|
|
(3.79) |
|
|
(3.80) |
|
h(x) = |
(3.81) |
| = | |||
| = | |||
| = | 0 | (3.82) |
L'équation dynamique s'écrit simplement pour g :
où
 |
(3.84) |
|
|
(3.85) |
Dans l'équation [![[*]](crossref.gif) ], le temps a été redimensionné par
4/
], le temps a été redimensionné par
4/![]() F
F![]() (3.7)
et les variables spatiales x et
(3.7)
et les variables spatiales x et ![]() , par
, par
![]()
![]() ; alors l'équation d'évolution du méandre ne dépend plus que d'un paramètre adimensionné :
; alors l'équation d'évolution du méandre ne dépend plus que d'un paramètre adimensionné :
![]() = DLa/DS
= DLa/DS![]() qui mesure l'importance de la diffusion de ligne relativement à la diffusion de terrasse.
qui mesure l'importance de la diffusion de ligne relativement à la diffusion de terrasse.
L'intégration numérique de l'équation du méandre [![[*]](crossref.gif) ]
conduit à l'émergence d'une structure cellulaire.
Les simulations sont effectuées en perturbant aléatoirement, avec un bruit blanc de faible amplitude, une marche initialement droite.
]
conduit à l'émergence d'une structure cellulaire.
Les simulations sont effectuées en perturbant aléatoirement, avec un bruit blanc de faible amplitude, une marche initialement droite.
La structure qui se développe est cellulaire.
Aucun mûrissement n'est observé : la longueur d'onde caractéristique de la structure formée reste celle sélectionnée aux premiers temps du développement de l'instabilité (voir fig. [![[*]](crossref.gif) ]) ; elle est proche de la longueur d'onde du mode le plus instable linéairement :
]) ; elle est proche de la longueur d'onde du mode le plus instable linéairement :
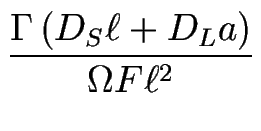 |
(3.86) |
|
|
Cependant, si ces résultats corroborent ceux obtenus précédemment par Pierre-Louis et al. [#!Pierre-Louis98a!#], l'intégration numérique de [![[*]](crossref.gif) ] avec le nouveaux schéma numérique présenté précédemment donne des résultats qualitativement différents
quant à la forme du méandre.
Si la structure qui se développe reste cellulaire, elle ne présente plus de singularités aux pointes
(voir fig. [
] avec le nouveaux schéma numérique présenté précédemment donne des résultats qualitativement différents
quant à la forme du méandre.
Si la structure qui se développe reste cellulaire, elle ne présente plus de singularités aux pointes
(voir fig. [![[*]](crossref.gif) ]).
]).
Les termes de relaxation sont maintenant bien pris en compte dans le nouveau schéma numérique adopté. La structure observée dans le cas de la relaxation par diffusion sur les terrasses (![]() = 0) a une morphologie en dents de scie (cf fig. [
= 0) a une morphologie en dents de scie (cf fig. [![[*]](crossref.gif) ]), comme reporté dans [#!Pierre-Louis98a!#] ; cependant, les pointes des cellules ne présentent pas de singularités. Les termes relaxants « adoucissent » le sommet des cellules.
]), comme reporté dans [#!Pierre-Louis98a!#] ; cependant, les pointes des cellules ne présentent pas de singularités. Les termes relaxants « adoucissent » le sommet des cellules.
La courbure maximum du méandre est atteinte au sommet des cellules mais reste finie.
Elle croît au cours du temps avant de saturer pour attendre une valeur
![]() , caractéristique du processus de relaxation mis en jeu (cf fig. [
, caractéristique du processus de relaxation mis en jeu (cf fig. [![[*]](crossref.gif) ]).
La diffusion de ligne réalise une meilleure relaxation du méandre que la diffusion de terrasse. Le rayon de courbure caractéristique des cellules augmente avec
]).
La diffusion de ligne réalise une meilleure relaxation du méandre que la diffusion de terrasse. Le rayon de courbure caractéristique des cellules augmente avec
![]() (où
(où
![]() = 1/(1 +
= 1/(1 + ![]() )). La diffusion de ligne conduit à une morphologie plus « adoucie » du méandre.
)). La diffusion de ligne conduit à une morphologie plus « adoucie » du méandre.
|
À temps plus long, les cellules qui caractérisent la structure du méandre prennent la forme de « doigts » allongés dont la taille croît comme t1/2 (voir fig. [![[*]](crossref.gif) -b)]).
L'extrémité de ces doigts ne présente aucune singularité à temps fini.
À l'échelle du méandre, elle se présente sous la forme d'un plateau qui atteint une
taille fixée après un régime transitoire
(voir fig. [
-b)]).
L'extrémité de ces doigts ne présente aucune singularité à temps fini.
À l'échelle du méandre, elle se présente sous la forme d'un plateau qui atteint une
taille fixée après un régime transitoire
(voir fig. [![[*]](crossref.gif) -a)]).
-a)]).
|
La forme des cellules et notamment la taille des plateaux dépend fortement du processus de
relaxation mis en jeu (par diffusion de terrasse ou
diffusion de ligne) comme montré sur la figure [![[*]](crossref.gif) ].
].
|
|
La dépendance de la taille des plateaux en fonction du paramètre ![]() , obtenue
numériquement peut être évaluée analytiquement.
Ce calcul
est développé dans la réf. [#!Gillet00a!#]. Nous en reportons ici les principales idées et résultats. L'idée principale s'appuie sur les observations numériques et consiste à décomposer le méandre en deux régions distinctes
pour lesquelles une approximation spécifique du méandre via une décomposition des variables sera cherchée.
Le fait, que la rugosité du méandre croît en loi de puissance comme t0, 5 alors que la courbure du sommet des cellules tend vers une valeur définie, laisse supposer que les parties latérales (de forte pente) des cellules subissent une dilatation au cours du temps alors que les sommets des cellules sont simplement advectés au loin.
Dans les régions de forte pente, on cherchera alors à exprimer le méandre sous la forme :
, obtenue
numériquement peut être évaluée analytiquement.
Ce calcul
est développé dans la réf. [#!Gillet00a!#]. Nous en reportons ici les principales idées et résultats. L'idée principale s'appuie sur les observations numériques et consiste à décomposer le méandre en deux régions distinctes
pour lesquelles une approximation spécifique du méandre via une décomposition des variables sera cherchée.
Le fait, que la rugosité du méandre croît en loi de puissance comme t0, 5 alors que la courbure du sommet des cellules tend vers une valeur définie, laisse supposer que les parties latérales (de forte pente) des cellules subissent une dilatation au cours du temps alors que les sommets des cellules sont simplement advectés au loin.
Dans les régions de forte pente, on cherchera alors à exprimer le méandre sous la forme :
|
|
(3.89) |
I( ![$\displaystyle {\frac{1}{[ U(1) - U(m)]^{1/2}}}$](img432.gif) dm , dm ,
|
(3.91) |
U(m) =  dm' . dm' .
|
(3.92) |
Le comportement de la largeur des plateaux en fonction du processus de relaxation trouvé analytiquement est en bon accord quantitatif avec les résultats obtenus à partir des simulations numériques (voir fig. [![[*]](crossref.gif) ]).
]).
![\includegraphics[width=10cm,angle=0]{../Images/plateau_size_beta.eps}](img435.gif)
|
Une autre caractéristique importante de la structure observée est sa symétrie, aussi bien dans la direction x, parallèle aux marches que dans la direction perpendiculaire z, celle de la vicinalité. Ces symétries sont présentes dans l'écriture de l'équation dynamique.
Aucune des simulations effectuées n'a donné lieu à une brisure de symétrie, que ce soit dans la direction x ou plus probablement dans la direction z.
La symétrie de la structure vis à vis de la transformation
z ![]() - z est surprenante car de par le fait que les marches avancent dans la direction z, le système n'est pas a priori invariant sous cette transformation (cela est directement visible sur l'écriture des équations constitutives du modèle BCF).
Cette symétrie est aussi en contradiction avec les expériences réalisées sur la croissance de surfaces vicinales de cuivre où le méandre observé ne possède pas cette symétrie.
Le fait est que la vitesse d'avancée des marches est proportionnelle à
- z est surprenante car de par le fait que les marches avancent dans la direction z, le système n'est pas a priori invariant sous cette transformation (cela est directement visible sur l'écriture des équations constitutives du modèle BCF).
Cette symétrie est aussi en contradiction avec les expériences réalisées sur la croissance de surfaces vicinales de cuivre où le méandre observé ne possède pas cette symétrie.
Le fait est que la vitesse d'avancée des marches est proportionnelle à ![]() , notre petit paramètre. Or le développement à l'ordre dominant effectué correspond formellement à la limite
, notre petit paramètre. Or le développement à l'ordre dominant effectué correspond formellement à la limite
![]()
![]() 0 ; à l'ordre dominant, l'asymétrie du système dans la direction z due à l'avancée des marches est supprimée. Pour pouvoir rendre compte d'une telle asymétrie dans la structure cellulaire du méandre il faut alors poursuivre le développement non linéaire aux ordres supérieurs afin de faire explicitement
apparaître
0 ; à l'ordre dominant, l'asymétrie du système dans la direction z due à l'avancée des marches est supprimée. Pour pouvoir rendre compte d'une telle asymétrie dans la structure cellulaire du méandre il faut alors poursuivre le développement non linéaire aux ordres supérieurs afin de faire explicitement
apparaître ![]() dans l'équation dynamique ; cela sera étudié dans la suite (voir §
dans l'équation dynamique ; cela sera étudié dans la suite (voir §![[*]](crossref.gif) ).
).