


suivant: Termes sous-dominants
monter: Méandre des marches en
précédent: Résultats numériques
Table des matières
Jusqu'à présent, nous avons supposé le modèle strictement unilatéral ; ce qui correspond à un attachement instantané des adatomes aux marches depuis la terrasse inférieure et à un attachement impossible depuis la terrasse supérieure.
Nous nous proposons maintenant d'abandonner cette hypothèse et de prendre en compte un effet Ehrlich-Schwoebel fini.
Dans ce régime que nous appellerons « bilatéral », une analyse d'échelle multiple similaire à celle effectuée dans le cas unilatéral peut être faite.
À l'ordre dominant, elle conduit à l'équation dynamique suivante pour l'évolution du méandre :
où la mobilité effective des adatomes s'écrit ici :
Bien que cette équation soit qualitativement différente de celle trouvée dans le cas unilatéral (que l'on peut retrouver en prenant la limite
d+ = 0 et
d-  +
+ 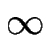 ), le comportement dynamique reste très similaire. Comme précédemment, une structure cellulaire prend naissance, conduisant à la formation de doigts allongés.
La longueur d'onde de cette structure correspond toujours à celle du mode le plus instable linéairement :
Comme
fs
), le comportement dynamique reste très similaire. Comme précédemment, une structure cellulaire prend naissance, conduisant à la formation de doigts allongés.
La longueur d'onde de cette structure correspond toujours à celle du mode le plus instable linéairement :
Comme
fs  1, la structure ici formée dans le cas bilatéral a une longueur d'onde plus grande que dans le cas unilatéral. Comme précédemment aussi, la relaxation par diffusion de ligne forme des structures plus « douces » qu'avec la diffusion de terrasse.
À temps long (i.e. pour plus de
400/fs
1, la structure ici formée dans le cas bilatéral a une longueur d'onde plus grande que dans le cas unilatéral. Comme précédemment aussi, la relaxation par diffusion de ligne forme des structures plus « douces » qu'avec la diffusion de terrasse.
À temps long (i.e. pour plus de
400/fs monocouches déposées), la rugosité du méandre suit une loi de puissance avec le même exposant que dans le cas unilatéral :
w
monocouches déposées), la rugosité du méandre suit une loi de puissance avec le même exposant que dans le cas unilatéral :
w  t1/2.
t1/2.
Figure:
Taille des plateaux en fonction de l'effet Ehrlich-Schwoebel. Les résultats analytiques sont représentés en trait plein, les symboles correspondent aux résultats numériques :
 se rapportent à la diffusion de terrasse tandis que
se rapportent à la diffusion de terrasse tandis que  concernent la diffusion de ligne.
concernent la diffusion de ligne.
|
|
De plus, aux extrémités des doigts, des plateaux apparaissent et comme précédemment, un calcul analytique permet de relier la taille de ces plateaux avec l'importance de l'effet Ehrlich-Schwoebel. Dans le cas où la diffusion de ligne domine le processus de relaxation (
DLa  DS
DS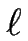 ), on a :
), on a :
où
 /2 est la taille des plateaux,
/2 est la taille des plateaux,
 =
= 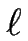 /(
/( + d+ + d-) et I est la même fonction que dans l'équation [
+ d+ + d-) et I est la même fonction que dans l'équation [![[*]](crossref.gif) ].
].
Dans le cas où la diffusion de terrasse domine les effets de relaxation (
DLa  DS
DS ), on trouve :
), on trouve :
De nouveau, ces résultats analytiques sont en bon accord avec le comportement obtenu numériquement (fig.[![[*]](crossref.gif) ]).
]).

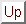


suivant: Termes sous-dominants
monter: Méandre des marches en
précédent: Résultats numériques
Table des matières
fred
2001-07-02


 + DLa
+ DLa
![\includegraphics[width=10cm,angle=0]{../Images/plateau_size_delta.eps}](img449.gif)
![]() DS
DS![]() ), on a :
), on a :
![[*]](crossref.gif) ].
].
![]() DS
DS![]() ), on trouve :
), on trouve :
![[*]](crossref.gif) ]).
]).