![\includegraphics[height=8cm,angle=0]{../Images/im_wr.eps}](img230.gif)
|
![\includegraphics[height=8cm,angle=0]{../Images/im_wr.eps}](img230.gif)
|
![[*]](crossref.gif) ].
Pour ces modes, on a
q
].
Pour ces modes, on a
q|
x |
(3.27) |
Le temps caractéristique de développement de l'instabilité est donné par le mode le plus instable (donc celui qui se développe le plus vite) :
Ce temps est obtenu à partir de la relation tm = 2![[*]](crossref.gif) ] fournit le comportement d'échelle de la variable temporelle :
t
] fournit le comportement d'échelle de la variable temporelle :
t
En utilisant les données expérimentales précédentes, on trouve que l'instabilité de méandre se développe après une croissance d'environ 2500 monocouches
3.4.
Avant d'aller plus loin, il est important d'analyser brièvement le cas du train de marches asynchrone.
L'effet Ehrlich-Schwoebel n'induit pas seulement une instabilité morphologique du profil des marches mais conduit aussi à une répulsion diffusive entre marches.
Cette répulsion dynamique force les marches à évoluer en phase.
Le temps t![]() , nécessaire aux marches pour s'organiser en phase dans le train de marches instable s'obtient facilement à partir du temps caractéristique de synchronisation du mode le plus instable.
Il est déterminé à partir de la relation de dispersion linéaire comme suit (c'est le préfacteur du terme en
, nécessaire aux marches pour s'organiser en phase dans le train de marches instable s'obtient facilement à partir du temps caractéristique de synchronisation du mode le plus instable.
Il est déterminé à partir de la relation de dispersion linéaire comme suit (c'est le préfacteur du terme en ![]() dans la partie réelle de
dans la partie réelle de ![]() ) :
) :
![$\displaystyle \left.\vphantom{ \partial_{\phi \phi} \Re e \left[ \omega(q,\phi) \right] \frac{}{} }\right\vert _{(q=q_m,\phi=0)}^{}$](img247.gif) . . |
(3.30) |
 |
(3.31) |
L'instabilité se développe donc pour un train de marches quasiment en phase.
Cela justifie que l'on considère, pour l'étude de l'instabilité, les petits déphasages (voire même le cas en phase).
Pour de petits déphasages ![]() , on a :
, on a :
| = | 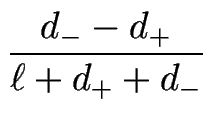 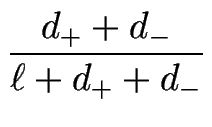 |
||
-  |
![[*]](crossref.gif) ]. Le domaine des modes actifs est délimité par
]. Le domaine des modes actifs est délimité par
En résumé, nous avons les lois d'échelle suivantes dans l'espace de Fourier :
|
q |
(3.32) |
Par-delà le problème de stabilité, la dynamique de la surface met en jeu des effets propagatifs liés au fait que les marches se déplacent et défilent le long de la surface.
Ceux-ci s'expriment dans la partie imaginaire de ![]() .
L'étude de la partie imaginaire de la relation de dispersion, dans la limite des grandes longueurs d'onde et petits déphasages montre que celle-ci se comporte comme
.
L'étude de la partie imaginaire de la relation de dispersion, dans la limite des grandes longueurs d'onde et petits déphasages montre que celle-ci se comporte comme
![]() .
Cela définit une échelle de temps rapide
.
Cela définit une échelle de temps rapide
![]()
![]()
![]() sur laquelle se produisent les effets propagatifs (rappelons que le développement de l'instabilité se fait sur une échelle de temps plus lente
sur laquelle se produisent les effets propagatifs (rappelons que le développement de l'instabilité se fait sur une échelle de temps plus lente
![]()
![]()
![]() ).
Dans un premier temps, nous nous focaliserons sur le cas en phase pour lequel les effets propagatifs disparaissent (la partie imaginaire de
).
Dans un premier temps, nous nous focaliserons sur le cas en phase pour lequel les effets propagatifs disparaissent (la partie imaginaire de ![]() est nulle dans ce cas) ; la dynamique est alors simplifiée et ne se fait plus que sur une seule échelle de temps, celle donnée par la partie réelle de
est nulle dans ce cas) ; la dynamique est alors simplifiée et ne se fait plus que sur une seule échelle de temps, celle donnée par la partie réelle de ![]() :
:
![]()
![]()
![]() .
Le cas plus délicat où la contrainte de synchronisation des marches est relaxée et où la dynamique du système s'effectue sur deux échelles de temps caractéristiques sera examiné ultérieurement au paragraphe
.
Le cas plus délicat où la contrainte de synchronisation des marches est relaxée et où la dynamique du système s'effectue sur deux échelles de temps caractéristiques sera examiné ultérieurement au paragraphe ![[*]](crossref.gif) .
.