


suivant: Méandre des marches en
monter: Analyse des échelles de
précédent: Échelles caractéristiques
Table des matières
Dans le but de déterminer l'équation non linéaire d'évolution des marches, nous devons déterminer le comportement d'échelle du méandre, c'est-à-dire la façon dont celui-ci se comporte en fonction du paramètre  .
Dans les premiers temps de développement de l'instabilité, la perturbation est extrêmement petite, seuls les termes linéaires sont pertinents pour la dynamique.
Cette dynamique linéaire des premiers temps de développement de l'instabilité produit une croissance exponentielle du méandre.
L'amplitude de celui-ci croît très rapidement et les non-linéarités du problème, négligeables initialement doivent alors être prises en compte.
Déterminer le comportement d'échelle du méandre c'est alors déterminer l'échelle
de l'amplitude du méandre pour laquelle les non-linéarités du système vont influer sur la dynamique.
Proche du seuil de l'instabilité,
.
Dans les premiers temps de développement de l'instabilité, la perturbation est extrêmement petite, seuls les termes linéaires sont pertinents pour la dynamique.
Cette dynamique linéaire des premiers temps de développement de l'instabilité produit une croissance exponentielle du méandre.
L'amplitude de celui-ci croît très rapidement et les non-linéarités du problème, négligeables initialement doivent alors être prises en compte.
Déterminer le comportement d'échelle du méandre c'est alors déterminer l'échelle
de l'amplitude du méandre pour laquelle les non-linéarités du système vont influer sur la dynamique.
Proche du seuil de l'instabilité,  est très petit comparé à l'unité.
Toutes les grandeurs caractéristiques de l'instabilité s'expriment alors en fonction de ce paramètre sous la forme de lois de puissances.
C'est cette loi de puissance que nous cherchons maintenant à déterminer pour l'amplitude critique du méandre.
Dans le cas où la désorption est présente, il a été trouvé [#!Bena93!#], [#!Pierre-Louis96!#], [#!Pierre-Louis98a!#], [#!Pierre-Louis98b!#] que le méandre se comporte comme
est très petit comparé à l'unité.
Toutes les grandeurs caractéristiques de l'instabilité s'expriment alors en fonction de ce paramètre sous la forme de lois de puissances.
C'est cette loi de puissance que nous cherchons maintenant à déterminer pour l'amplitude critique du méandre.
Dans le cas où la désorption est présente, il a été trouvé [#!Bena93!#], [#!Pierre-Louis96!#], [#!Pierre-Louis98a!#], [#!Pierre-Louis98b!#] que le méandre se comporte comme  ; cela signifie qu'un développement régulier de ce dernier est possible.
Dans le cas présent, où la désorption est absente, le scénario est différent ; le méandre se comporte comme
; cela signifie qu'un développement régulier de ce dernier est possible.
Dans le cas présent, où la désorption est absente, le scénario est différent ; le méandre se comporte comme
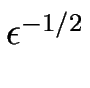 .
Aucun développement régulier du méandre ne conduit à l'émergence de termes non linéaires dans l'équation dynamique ; on parle alors de développement singulier.
Cela ne signifie pas pour autant que la dynamique elle même est singulière.
Dans le cas où la désorption est absente, les non-linéarités présentes dans le modèle ne sont pas assez fortes pour influer la dynamique aux tous premiers temps de développement de l'instabilité ; il faut attendre que le méandre ait atteint une amplitude importante (
.
Aucun développement régulier du méandre ne conduit à l'émergence de termes non linéaires dans l'équation dynamique ; on parle alors de développement singulier.
Cela ne signifie pas pour autant que la dynamique elle même est singulière.
Dans le cas où la désorption est absente, les non-linéarités présentes dans le modèle ne sont pas assez fortes pour influer la dynamique aux tous premiers temps de développement de l'instabilité ; il faut attendre que le méandre ait atteint une amplitude importante (


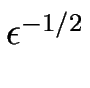 ) pour que leur influence sur la dynamique devienne pertinente.
Ce qui est intéressant c'est qu'alors on n'obtient plus un développement hiérarchique de termes non linéaires mais une équation elle même fortement non linéaire.
Rappelons que dans le cas où la désorption est présente, les non-linéarités présentes dans le modèle sont plus fortes et saturent très tôt le développement exponentiel de l'instabilité (dès que
) pour que leur influence sur la dynamique devienne pertinente.
Ce qui est intéressant c'est qu'alors on n'obtient plus un développement hiérarchique de termes non linéaires mais une équation elle même fortement non linéaire.
Rappelons que dans le cas où la désorption est présente, les non-linéarités présentes dans le modèle sont plus fortes et saturent très tôt le développement exponentiel de l'instabilité (dès que


 ).
Les non-linéarités apparaissent alors de façon hiérarchique que l'on peut tronquer à l'ordre dominant.
L'équation d'évolution non linéaire du méandre peut alors se décomposer dans ce cas en une partie linéaire (correspondant à la relation de dispersion linéaire) à laquelle vient s'ajouter une partie non linéaire.
).
Les non-linéarités apparaissent alors de façon hiérarchique que l'on peut tronquer à l'ordre dominant.
L'équation d'évolution non linéaire du méandre peut alors se décomposer dans ce cas en une partie linéaire (correspondant à la relation de dispersion linéaire) à laquelle vient s'ajouter une partie non linéaire.
Nous avons fourni [#!Gillet00a!#] un argument permettant d'expliquer comment le comportement d'échelle particulier du méandre est intimement lié au cas sans désorption sans avoir recours à une dérivation explicite des équations de la dynamique. Reportons en ici les principaux développements.
Dans ce but, il est utile d'identifier deux « classes » d'adatomes.
Tout d'abord les adatomes « fraîchement adsorbés », de concentration cF sont ceux qui viennent d'atterrir sur les terrasses ; ils n'ont pas encore été absorbés par les marches.
Ce sont eux qui sont responsables de par leur attachement aux marches de la déstabilisation hors équilibre du train de marche.
La seconde classe d'adatome correspond à des adatomes déjà absorbés par la surface, de concentration cT, nous les qualifierons « d'adatomes thermiques ».
Ils peuvent se détacher des marches, diffuser sur les terrasses et se rattacher ailleurs.
Le courant de matière associé à leur mouvement induit un processus de relaxation de la surface vers l'équilibre.
Les équations constitutives du modèle peuvent alors se décomposer en deux parties correspondant pour l'une aux effets déstabilisants et pour l'autre aux effets stabilisants :
D cT cT |
= |
0, |
(3.34) |
D cF cF |
= |
- F. |
(3.35) |
Ces deux champs de concentration obéissent aux conditions limites suivantes aux bords des terrasses :
D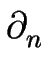 cT cT |
= |
± (cT - ceq) , (cT - ceq) , |
(3.36) |
D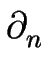 cF cF |
= |
± cF , cF , |
(3.37) |
où les indices + et - se réfèrent respectivement à chacun des cotés de la marche dont il est question.
Ils sont seulement couplés à travers la relation de conservation de la matière aux marches :
où la contribution vF à la vitesse normale de la marche Vn est proportionnelle au flux atomique incident F.
Elle est déterminée par la différence de gradient :
vF = D[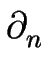 cF+ - cF+ - 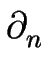 cF-]. cF-].
|
(3.39) |
En effectuant la transformation
cF  cF/F, on s'aperçoit que les équations concernant cF deviennent indépendantes du flux incident F ; cela implique que cF doit être directement proportionnel à F.
On peut extraire de cF la contribution provenant du train de marches non perturbé.
Celle-ci apporte dans l'expression de la vitesse Vn une contribution donnée par
cF/F, on s'aperçoit que les équations concernant cF deviennent indépendantes du flux incident F ; cela implique que cF doit être directement proportionnel à F.
On peut extraire de cF la contribution provenant du train de marches non perturbé.
Celle-ci apporte dans l'expression de la vitesse Vn une contribution donnée par
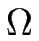 F
F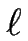 qui correspond à la vitesse moyenne du train de marches.
La partie restante de cF, due aux modulations des marches doit être compatible avec la loi de conservation globale de la matière.
vF se décompose donc en une partie donnant la vitesse moyenne du train de marche et une partie qui s'écrit comme la divergence d'un flux et qui décrit la façon dont la matière se répartit entre les différentes marches et les différentes parties d'une même marche :
j étant, comme nous l'avons fait remarquer plus haut, indépendant de F.
qui correspond à la vitesse moyenne du train de marches.
La partie restante de cF, due aux modulations des marches doit être compatible avec la loi de conservation globale de la matière.
vF se décompose donc en une partie donnant la vitesse moyenne du train de marche et une partie qui s'écrit comme la divergence d'un flux et qui décrit la façon dont la matière se répartit entre les différentes marches et les différentes parties d'une même marche :
j étant, comme nous l'avons fait remarquer plus haut, indépendant de F.
La contribution de relaxation vT provient des adatomes thermalisés avec la surface et est donc indépendante de F :
vT = [D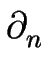 cT]+- + a cT]+- + a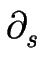 [DL [DL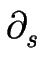 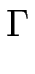 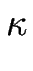 ]. ].
|
(3.41) |
La force thermodynamique responsable de la contribution relaxante à la vitesse est donnée par les gradients de potentiel chimique  .
Sans perte de généralité, et parce que nous considérons des perturbations douces et de grande échelle, la partie « thermique » de la vitesse normale peut s'écrire à l'aide de l'équation de Cahn-Hilliard [#!Cahn58!#] :
où
.
Sans perte de généralité, et parce que nous considérons des perturbations douces et de grande échelle, la partie « thermique » de la vitesse normale peut s'écrire à l'aide de l'équation de Cahn-Hilliard [#!Cahn58!#] :
où 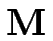 est la mobilité macroscopique de la surface et
est la mobilité macroscopique de la surface et
 =
= 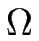
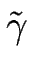
 est le potentiel chimique.
L'indice des marches a été omis ici afin de simplifier les notations.
À partir de maintenant, nous utiliserons donc la mobilité scalaire M le long de x.
Le potentiel chimique s'écrit
est le potentiel chimique.
L'indice des marches a été omis ici afin de simplifier les notations.
À partir de maintenant, nous utiliserons donc la mobilité scalaire M le long de x.
Le potentiel chimique s'écrit
 =
= 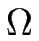
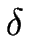
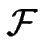 /
/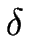
 , où
, où 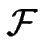 est l'énergie libre des marches.
Ainsi, si f est la densité d'énergie libre, on a :
L'équation d'évolution du méandre (i.e. lorsque la vitesse moyenne des marches a été soustraite) s'écrit maintenant :
F étant proportionnel à
est l'énergie libre des marches.
Ainsi, si f est la densité d'énergie libre, on a :
L'équation d'évolution du méandre (i.e. lorsque la vitesse moyenne des marches a été soustraite) s'écrit maintenant :
F étant proportionnel à  , on peut poser
F =
, on peut poser
F = 
 , où
, où  est d'ordre un.
De plus, l'instabilité se produisant pour les grandes longueurs d'onde
x =
est d'ordre un.
De plus, l'instabilité se produisant pour les grandes longueurs d'onde
x = 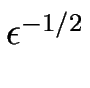 X, on a
X, on a
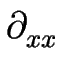 =
= 
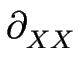 .
À cause de l'invariance du problème par translation, j, m et f' ne dépendent que des dérivées de
.
À cause de l'invariance du problème par translation, j, m et f' ne dépendent que des dérivées de  .
Nous écrirons leurs arguments symboliquement sous la forme
{
.
Nous écrirons leurs arguments symboliquement sous la forme
{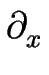 } = {
} = {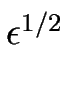
 } pour indiquer que toutes les dérivées peuvent être présentes.
L'équation précédente peut se récrire :
} pour indiquer que toutes les dérivées peuvent être présentes.
L'équation précédente peut se récrire :
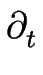  = - = -   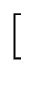   j{ j{  } + M{ } + M{  } }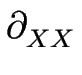 f'{ f'{  } }![$\displaystyle \left.\vphantom{
\Omega \bar{F}j\{\epsilon^{1/2}\partial_X\}+ M\{\epsilon^{1/2}\partial_X\}
\partial_{XX}f'\{\epsilon^{1/2}\partial_X\}}\right]$](img285.gif) . .
|
(3.45) |
Le point important tient au fait que le petit paramètre  apparaît comme facteur commun ; dans le premier terme du membre de droite, il provient du flux F alors que dans le second, il est produit par la dérivée seconde.
apparaît comme facteur commun ; dans le premier terme du membre de droite, il provient du flux F alors que dans le second, il est produit par la dérivée seconde.
Intéressons nous maintenant au comportement d'échelle du méandre. Posons
 =
= 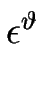 H où H est d'ordre un.
Nous allons maintenant montrer que le méandre suit une loi d'échelle singulière en absence de désorption.
Supposons tout d'abord
H où H est d'ordre un.
Nous allons maintenant montrer que le méandre suit une loi d'échelle singulière en absence de désorption.
Supposons tout d'abord
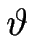 > - 1/2, alors toutes les fonctions du problème dépendantes de
> - 1/2, alors toutes les fonctions du problème dépendantes de  peuvent être développées régulièrement.
Soit h une telle fonction (qui peut représenter le flux j mais aussi la mobilité M ou la densité d'énergie f), son développement en série de Taylor autour de la valeur non perturbée est régulier :
peuvent être développées régulièrement.
Soit h une telle fonction (qui peut représenter le flux j mais aussi la mobilité M ou la densité d'énergie f), son développement en série de Taylor autour de la valeur non perturbée est régulier :
h = h0 + h1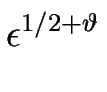 ( ( H) + h2 H) + h2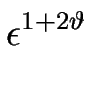 ( ( H)2 + h.o.t. , H)2 + h.o.t. ,
|
(3.46) |
où nous n'avons gardé que les contributions d'ordre supérieur.
En rendant explicite l'échelle temporelle (
T =  t), l'équation d'évolution du méandre s'écrit, en prenant en considération les développement précédents :
t), l'équation d'évolution du méandre s'écrit, en prenant en considération les développement précédents :
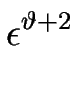  H = - H = - 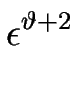   j1 j1 H + H + 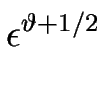 j2( j2( H)2 H)2 |
|
|
|
 + +  M0 + M0 + 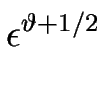 M1 M1 H H 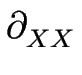 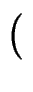 f1' f1' H + H + 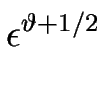 f2'( f2'( H)2 H)2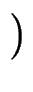 ![$\displaystyle \left.\vphantom{
+ \left( M_0 + \epsilon^{\vartheta+1/2} M_1\part...
...(f_1'\partial_X H
+\epsilon^{\vartheta+1/2} f_2'(\partial_XH)^2\right) }\right]$](img300.gif) + h.o.t. + h.o.t. |
|
|
(3.47) |
Si
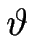 > - 1/2, on s'aperçoit qu'à l'ordre dominant, les termes non linéaires disparaissent et l'équation d'évolution se réduit à une équation linéaire :
> - 1/2, on s'aperçoit qu'à l'ordre dominant, les termes non linéaires disparaissent et l'équation d'évolution se réduit à une équation linéaire :
 H = - j1 H = - j1 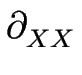 H - M0 f1' H - M0 f1' 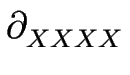 H . H .
|
(3.48) |
Pour que les non-linéarités soient pertinentes dans l'équation [![[*]](crossref.gif) ], il faut que
], il faut que
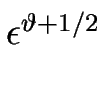
 O(1) ; ce qui est obtenu pour
O(1) ; ce qui est obtenu pour
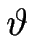 = - 1/2.
Mais alors, le développement de Taylor effectué dans l'équation [
= - 1/2.
Mais alors, le développement de Taylor effectué dans l'équation [![[*]](crossref.gif) ] n'est plus possible.
On s'attend à obtenir pour la dynamique, une équation fortement non linéaire.
] n'est plus possible.
On s'attend à obtenir pour la dynamique, une équation fortement non linéaire.
Le comportement d'échelle du champ de concentration en fonction de  peut lui aussi être obtenu à partir de la décomposition précédente.
À partir des équations [
peut lui aussi être obtenu à partir de la décomposition précédente.
À partir des équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ], nous avons
], nous avons
et en utilisant les équations [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] on trouve que :
] on trouve que :
cT - ceq0  ceq - ceq0 ceq - ceq0  ceq0 ceq0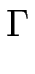 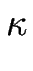   , ,
|
(3.50) |
car


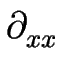


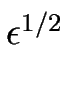 .
Ainsi, le champ de concentration réduit u défini par
u =
.
Ainsi, le champ de concentration réduit u défini par
u = 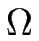 (cF + cT - ceq0) comme le taux de couverture réduit, est d'ordre
(cF + cT - ceq0) comme le taux de couverture réduit, est d'ordre
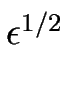 .
Nous l'écrirons sous la forme :
.
Nous l'écrirons sous la forme :
u(x, z, t) =  U(x, z, t) , U(x, z, t) ,
|
(3.51) |
où U est une fonction d'ordre un. De la même manière, le méandre se récrit :
 (x, t) = (x, t) = 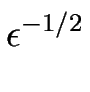 H(x, t) , H(x, t) ,
|
(3.52) |
H étant d'ordre un.
Il est important maintenant de montrer pourquoi, en présence de désorption, le développement du méandre est régulier et conduit à l'équation de Kuramoto-Shivashinsky.
En présence de désorption, l'équation d'évolution n'a plus de raison de s'écrire sous la forme d'une loi de conservation.
Néanmoins, la décomposition utilisée précédemment est encore valable sous une forme légèrement différente : la partie déstabilisante n'est plus proportionnelle au flux F mais à l'écart par rapport au flux d'équilibre F - Feq ; Feq étant le flux incident à l'équilibre, qui contrebalance la désorption des adatomes de la surface (
Feq = ceq0/ où
où  est le temps caractéristique de présence des adatomes sur la surface avant désorption).
Ainsi, à la place de l'équation [
est le temps caractéristique de présence des adatomes sur la surface avant désorption).
Ainsi, à la place de l'équation [![[*]](crossref.gif) ], nous avons :
], nous avons :
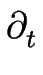  = (Feq - F)g + N = (Feq - F)g + N  f' , f' ,
|
(3.53) |
où g et N sont des fonctions des dérivées de  .
Le second terme du membre de droite est maintenant celui attendu pour une relaxation vers l'équilibre dans un système non conservé : il est directement proportionnel à la différence de potentiel chimique
.
Le second terme du membre de droite est maintenant celui attendu pour une relaxation vers l'équilibre dans un système non conservé : il est directement proportionnel à la différence de potentiel chimique



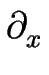 f' entre la phase solide et la phase vapeur.
L'expression précédente peut être linéarisée autour de la marche droite en ne conservant que les termes compatibles avec les symétries du problème3.5.
L'équation [
f' entre la phase solide et la phase vapeur.
L'expression précédente peut être linéarisée autour de la marche droite en ne conservant que les termes compatibles avec les symétries du problème3.5.
L'équation [![[*]](crossref.gif) ] développée prend alors la forme :
] développée prend alors la forme :
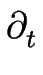  = [(Feq - F) = [(Feq - F)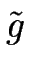 + N0 f'1] + N0 f'1] 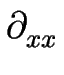  . .
|
(3.54) |
Une valeur négative du préfacteur de la dérivée seconde conduit à une instabilité de la marche.
Cela se produit lorsque F > Fc, avec
Fc = Feq + N0 f'1/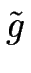 .
Le paramètre donnant l'écart par rapport au seuil de l'instabilité est maintenant
.
Le paramètre donnant l'écart par rapport au seuil de l'instabilité est maintenant

 F - Fc.
Les échelles spatiales et temporelles sont comme précédemment définies à partir de l'étude linéaire ; et dans le cas présent on a :
x
F - Fc.
Les échelles spatiales et temporelles sont comme précédemment définies à partir de l'étude linéaire ; et dans le cas présent on a :
x 
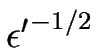 et
t
et
t 
 (cf. [#!Bena93!#,#!Pierre-Louis98b!#]).
En définissant comme dans le cas conservé des variables adimensionnées X, T et H d'ordre 1 en
(cf. [#!Bena93!#,#!Pierre-Louis98b!#]).
En définissant comme dans le cas conservé des variables adimensionnées X, T et H d'ordre 1 en  telles que
X =
telles que
X = 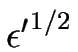 x,
T =
x,
T = 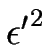 t et
t et
 =
= 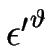 H, l'équation [
H, l'équation [![[*]](crossref.gif) ] se développe proche du seuil de l'instabilité (
F
] se développe proche du seuil de l'instabilité (
F  Fc) sous la forme suivante :
Fc) sous la forme suivante :
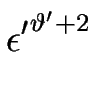  H = - H = - 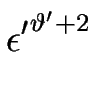  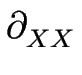 H + H + 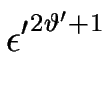 (F - Feq) ( (F - Feq) ( H)2 g2 H)2 g2 |
|
|
|
+ 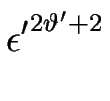  N0 f2' N0 f2' 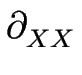 ( ( H)2 + N1 f1' H)2 + N1 f1'  H H 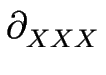 H H![$\displaystyle \left.\vphantom{
N_0 \, f_2' \, \partial_{XX} \, (\partial_X H)^2
+ N_1 \, f_1' \, \partial_X H \, \partial_{XXX} H
}\right]$](img316.gif) + h.o.t. . + h.o.t. . |
|
|
(3.55) |
Pour
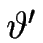 > - 1/2, le développement hiérarchique [
> - 1/2, le développement hiérarchique [![[*]](crossref.gif) ] est valide.
En l'insérant dans l'expression précédente, on peut identifier le terme non linéaire dominant :
(F - Feq)
] est valide.
En l'insérant dans l'expression précédente, on peut identifier le terme non linéaire dominant :
(F - Feq)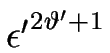 (
( H)2. Il contrebalance le terme linéaire
H)2. Il contrebalance le terme linéaire
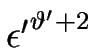
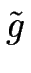
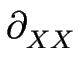 H dès que
H dès que
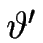 = 1.
Le développement de l'amplitude du méandre est dans ce cas régulier.
Le terme non linéaire est celui des équations de Kadar-Parisi-Zhang et Kuramoto-Sivashinsky.
Il ne peut être présent dans le cas conservé car il ne peut s'écrire sous la forme de la divergence d'un flux.
Il est non variationnel et doit disparaître à l'équilibre ; ce qui est visible sur son préfacteur F - Feq.
= 1.
Le développement de l'amplitude du méandre est dans ce cas régulier.
Le terme non linéaire est celui des équations de Kadar-Parisi-Zhang et Kuramoto-Sivashinsky.
Il ne peut être présent dans le cas conservé car il ne peut s'écrire sous la forme de la divergence d'un flux.
Il est non variationnel et doit disparaître à l'équilibre ; ce qui est visible sur son préfacteur F - Feq.



suivant: Méandre des marches en
monter: Analyse des échelles de
précédent: Échelles caractéristiques
Table des matières
fred
2001-07-02
![]() .
Dans les premiers temps de développement de l'instabilité, la perturbation est extrêmement petite, seuls les termes linéaires sont pertinents pour la dynamique.
Cette dynamique linéaire des premiers temps de développement de l'instabilité produit une croissance exponentielle du méandre.
L'amplitude de celui-ci croît très rapidement et les non-linéarités du problème, négligeables initialement doivent alors être prises en compte.
Déterminer le comportement d'échelle du méandre c'est alors déterminer l'échelle
de l'amplitude du méandre pour laquelle les non-linéarités du système vont influer sur la dynamique.
Proche du seuil de l'instabilité,
.
Dans les premiers temps de développement de l'instabilité, la perturbation est extrêmement petite, seuls les termes linéaires sont pertinents pour la dynamique.
Cette dynamique linéaire des premiers temps de développement de l'instabilité produit une croissance exponentielle du méandre.
L'amplitude de celui-ci croît très rapidement et les non-linéarités du problème, négligeables initialement doivent alors être prises en compte.
Déterminer le comportement d'échelle du méandre c'est alors déterminer l'échelle
de l'amplitude du méandre pour laquelle les non-linéarités du système vont influer sur la dynamique.
Proche du seuil de l'instabilité, ![]() est très petit comparé à l'unité.
Toutes les grandeurs caractéristiques de l'instabilité s'expriment alors en fonction de ce paramètre sous la forme de lois de puissances.
C'est cette loi de puissance que nous cherchons maintenant à déterminer pour l'amplitude critique du méandre.
Dans le cas où la désorption est présente, il a été trouvé [#!Bena93!#], [#!Pierre-Louis96!#], [#!Pierre-Louis98a!#], [#!Pierre-Louis98b!#] que le méandre se comporte comme
est très petit comparé à l'unité.
Toutes les grandeurs caractéristiques de l'instabilité s'expriment alors en fonction de ce paramètre sous la forme de lois de puissances.
C'est cette loi de puissance que nous cherchons maintenant à déterminer pour l'amplitude critique du méandre.
Dans le cas où la désorption est présente, il a été trouvé [#!Bena93!#], [#!Pierre-Louis96!#], [#!Pierre-Louis98a!#], [#!Pierre-Louis98b!#] que le méandre se comporte comme ![]() ; cela signifie qu'un développement régulier de ce dernier est possible.
Dans le cas présent, où la désorption est absente, le scénario est différent ; le méandre se comporte comme
; cela signifie qu'un développement régulier de ce dernier est possible.
Dans le cas présent, où la désorption est absente, le scénario est différent ; le méandre se comporte comme
![]() .
Aucun développement régulier du méandre ne conduit à l'émergence de termes non linéaires dans l'équation dynamique ; on parle alors de développement singulier.
Cela ne signifie pas pour autant que la dynamique elle même est singulière.
Dans le cas où la désorption est absente, les non-linéarités présentes dans le modèle ne sont pas assez fortes pour influer la dynamique aux tous premiers temps de développement de l'instabilité ; il faut attendre que le méandre ait atteint une amplitude importante (
.
Aucun développement régulier du méandre ne conduit à l'émergence de termes non linéaires dans l'équation dynamique ; on parle alors de développement singulier.
Cela ne signifie pas pour autant que la dynamique elle même est singulière.
Dans le cas où la désorption est absente, les non-linéarités présentes dans le modèle ne sont pas assez fortes pour influer la dynamique aux tous premiers temps de développement de l'instabilité ; il faut attendre que le méandre ait atteint une amplitude importante (
![]()
![]()
![]() ) pour que leur influence sur la dynamique devienne pertinente.
Ce qui est intéressant c'est qu'alors on n'obtient plus un développement hiérarchique de termes non linéaires mais une équation elle même fortement non linéaire.
Rappelons que dans le cas où la désorption est présente, les non-linéarités présentes dans le modèle sont plus fortes et saturent très tôt le développement exponentiel de l'instabilité (dès que
) pour que leur influence sur la dynamique devienne pertinente.
Ce qui est intéressant c'est qu'alors on n'obtient plus un développement hiérarchique de termes non linéaires mais une équation elle même fortement non linéaire.
Rappelons que dans le cas où la désorption est présente, les non-linéarités présentes dans le modèle sont plus fortes et saturent très tôt le développement exponentiel de l'instabilité (dès que
![]()
![]()
![]() ).
Les non-linéarités apparaissent alors de façon hiérarchique que l'on peut tronquer à l'ordre dominant.
L'équation d'évolution non linéaire du méandre peut alors se décomposer dans ce cas en une partie linéaire (correspondant à la relation de dispersion linéaire) à laquelle vient s'ajouter une partie non linéaire.
).
Les non-linéarités apparaissent alors de façon hiérarchique que l'on peut tronquer à l'ordre dominant.
L'équation d'évolution non linéaire du méandre peut alors se décomposer dans ce cas en une partie linéaire (correspondant à la relation de dispersion linéaire) à laquelle vient s'ajouter une partie non linéaire.
![]() =
= ![]() H où H est d'ordre un.
Nous allons maintenant montrer que le méandre suit une loi d'échelle singulière en absence de désorption.
Supposons tout d'abord
H où H est d'ordre un.
Nous allons maintenant montrer que le méandre suit une loi d'échelle singulière en absence de désorption.
Supposons tout d'abord
![]() > - 1/2, alors toutes les fonctions du problème dépendantes de
> - 1/2, alors toutes les fonctions du problème dépendantes de ![]() peuvent être développées régulièrement.
Soit h une telle fonction (qui peut représenter le flux j mais aussi la mobilité M ou la densité d'énergie f), son développement en série de Taylor autour de la valeur non perturbée est régulier :
peuvent être développées régulièrement.
Soit h une telle fonction (qui peut représenter le flux j mais aussi la mobilité M ou la densité d'énergie f), son développement en série de Taylor autour de la valeur non perturbée est régulier :
![[*]](crossref.gif) ], il faut que
], il faut que
![[*]](crossref.gif) ] n'est plus possible.
On s'attend à obtenir pour la dynamique, une équation fortement non linéaire.
] n'est plus possible.
On s'attend à obtenir pour la dynamique, une équation fortement non linéaire.
![]() peut lui aussi être obtenu à partir de la décomposition précédente.
À partir des équations [
peut lui aussi être obtenu à partir de la décomposition précédente.
À partir des équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ], nous avons
], nous avons
![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] on trouve que :
] on trouve que :
![]() où
où ![]() est le temps caractéristique de présence des adatomes sur la surface avant désorption).
Ainsi, à la place de l'équation [
est le temps caractéristique de présence des adatomes sur la surface avant désorption).
Ainsi, à la place de l'équation [![[*]](crossref.gif) ], nous avons :
], nous avons :
![[*]](crossref.gif) ] développée prend alors la forme :
] développée prend alors la forme :
![[*]](crossref.gif) ] se développe proche du seuil de l'instabilité (
F
] se développe proche du seuil de l'instabilité (
F ![[*]](crossref.gif) ] est valide.
En l'insérant dans l'expression précédente, on peut identifier le terme non linéaire dominant :
(F - Feq)
] est valide.
En l'insérant dans l'expression précédente, on peut identifier le terme non linéaire dominant :
(F - Feq)