![[*]](crossref.gif) ] que le mode le plus rapide à se développer est un mode en phase.
C'est ce mode qui influence le plus grandement la dynamique lors du développement de l'instabilité.
] que le mode le plus rapide à se développer est un mode en phase.
C'est ce mode qui influence le plus grandement la dynamique lors du développement de l'instabilité.
Nous avons vu, en étudiant la relation de dispersion linéaire [![[*]](crossref.gif) ] que le mode le plus rapide à se développer est un mode en phase.
C'est ce mode qui influence le plus grandement la dynamique lors du développement de l'instabilité.
] que le mode le plus rapide à se développer est un mode en phase.
C'est ce mode qui influence le plus grandement la dynamique lors du développement de l'instabilité.
Nous avons aussi vu que, proche du seuil de l'instabilité, les modes actifs (ceux pour lesquels
![]() e(
e(![]() ) > 0) se trouvent dans un voisinage du mode le plus instable
M(q = qm,
) > 0) se trouvent dans un voisinage du mode le plus instable
M(q = qm,![]() = 0), d'extension
= 0), d'extension
![]() q
q ![]()
![]() ,
,
![]()
![]()
![]()
![]() (voir figure [
(voir figure [![[*]](crossref.gif) ]).
]).
![\includegraphics[height=8cm,angle=0]{../Images/im_wr.eps}](img230.gif)
|
Jusqu'à présent, nous avons fait l'hypothèse que la dynamique du méandre se fait en phase. Cela constitue a priori une bonne approximation de la dynamique de la surface sur des échelles
![]()
![]()
![]() /
/![]() le long de la direction vicinale.
Cependant, l'étude de la dynamique de la surface vicinale à grande échelle nécessite de prendre en compte l'existence d'une distribution de phase dans les modes actifs de l'instabilité (i.e. de prendre en compte l'existence d'un déphasage entre marches qui bien que faible entre marches adjacentes (
le long de la direction vicinale.
Cependant, l'étude de la dynamique de la surface vicinale à grande échelle nécessite de prendre en compte l'existence d'une distribution de phase dans les modes actifs de l'instabilité (i.e. de prendre en compte l'existence d'un déphasage entre marches qui bien que faible entre marches adjacentes (
![]()
![]()
![]() ) devient d'ordre 1 à grande distance
) devient d'ordre 1 à grande distance
![]()
![]()
![]() /
/![]() ).
).
Dans ce paragraphe, nous nous proposons d'étudier la dynamique de la surface vicinale lorsque la contrainte de synchronisme du train de marches est relaxée ; c'est-à-dire lorsque l'on accorde au méandre, une liberté de phase.
Comme dans le cas en phase, on peut, proche du seuil de l'instabilité, dériver des équations microscopiques du modèle BCF, l'équation d'évolution pertinente décrivant la dynamique de la surface.
Le calcul reste similaire au cas en phase si ce n'est que l'existence d'un déphasage entre marches introduit, comme nous l'avons évoqué page ![[*]](crossref.gif) , une échelle de temps supplémentaire associée à la partie imaginaire de la pulsation
, une échelle de temps supplémentaire associée à la partie imaginaire de la pulsation ![]() et qui décrit la propagation de la perturbation dans le train de marches.
et qui décrit la propagation de la perturbation dans le train de marches.
Afin de prendre en compte le déphasage ![]() entre marches, nous introduisons l'opérateur
entre marches, nous introduisons l'opérateur ![]() de différence finie, défini, pour une fonction fm dépendant de l'indice des marches m, par :
de différence finie, défini, pour une fonction fm dépendant de l'indice des marches m, par :
|
|
(3.111) |
|
|
(3.112) |
Le détail des calculs est relégué en annexe ![[*]](crossref.gif) et conduit à l'équation dynamique suivante pour le méandre de la marche m :
et conduit à l'équation dynamique suivante pour le méandre de la marche m :
| Jm | = | 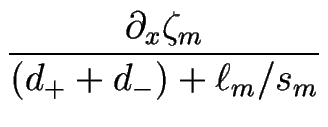 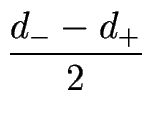 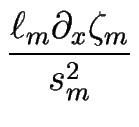 |
|
| - |
(3.114) | ||
| Gm | = | 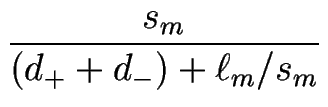 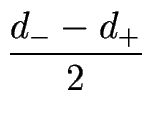 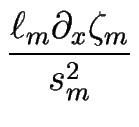 |
|
| (3.115) |
L'approximation « en phase » se retrouve à partir de l'équation [![[*]](crossref.gif) ] en prenant formellement
] en prenant formellement
![]() = 0.
= 0.
Nous avons obtenu l'équation dynamique pour la marche m.
Cette équation est couplée avec celle de la marche m + 1 et de proche en proche, avec toutes les marches de la surface
3.10.
La description de la dynamique de la surface reste, à ce stade, discrète : elle se fait par la description de la dynamique de chacune des marches qui la compose.
Ce que nous désirons, c'est une description continue, à grande échelle de la surface.
Une telle description continue peut être obtenue en poursuivant le développement analytique. Le détail des calculs figure en annexe ![[*]](crossref.gif) ; donnons-en ici quelques lignes directrices.
; donnons-en ici quelques lignes directrices.
Considérons que la surface peut être représentée dans le repère fixe du laboratoire par une équation de la forme :
| f (x, y, z, t) = 0 . | (3.116) |
|
f (x, y, z, t) = 0 = z - |
(3.117) |
Nous pouvons aussi choisir une représentation continue de la surface au moyen d'une fonction h de x et z qui représente la hauteur de la surface en (x, z). Nous avons alors :
| f (x, y, z, t) = 0 = y - h(x, z, t) . | (3.118) |
À
z = ![]() (x, t) et y = - ma (c'est-à-dire, le long d'une marche), nous avons la correspondance suivante entre les deux représentations :
(x, t) et y = - ma (c'est-à-dire, le long d'une marche), nous avons la correspondance suivante entre les deux représentations :
|
h(x, V0t + m |
(3.119) |
![[*]](crossref.gif) ] dynamiques de la représentation discrète en une équation d'évolution continue.
] dynamiques de la représentation discrète en une équation d'évolution continue.
L'équation dynamique pertinente décrivant la dynamique à grande échelle de la surface vicinale prend la forme suivante pour la hauteur de la surface :
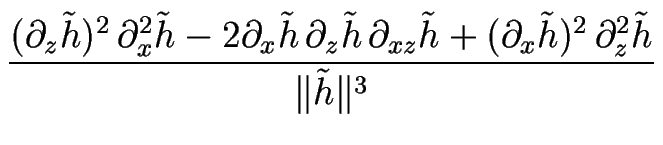 , ,
|
(3.120) |
Les vecteurs ![]() et
et ![]() sont définis par :
sont définis par :
| = | 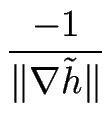  |
(3.121) | |
| = |  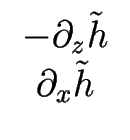 |
(3.122) |
En faisant intervenir le potentiel chimique
![]() = kBT
= kBT ![]()
![]() , l'équation de la surface [
, l'équation de la surface [![[*]](crossref.gif) ] se récrit simplement :
] se récrit simplement :
| = | 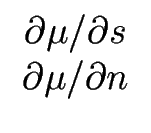 |
||
| = | ( |
(3.124) |
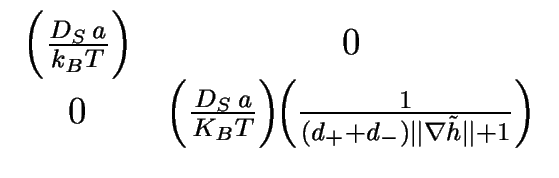 |
(3.125) |
Comme dans le cas en phase, le développement de l'équation d'évolution de la surface peut être poursuivi à l'ordre supérieur.
Le calcul a été effectué dans la limite unilatérale (
d+ = 0, d- ![]() +
+ ![]() ) et l'équation dynamique de la surface, incluant les termes sous-dominants est présentée en annexe
) et l'équation dynamique de la surface, incluant les termes sous-dominants est présentée en annexe ![[*]](crossref.gif) .
Cela nous a permis d'identifier, dans la limite unilatérale, la contribution d'ordre supérieur à la mobilité effective
.
Cela nous a permis d'identifier, dans la limite unilatérale, la contribution d'ordre supérieur à la mobilité effective
![]() :
:
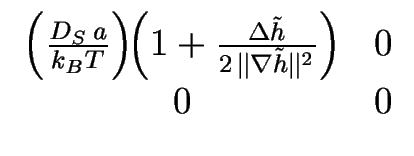 |
(3.126) |