



suivant: Méandre avec liberté de
monter: Méandre des marches en
précédent: Termes sous-dominants
Table des matières
Un adatome ou défaut ponctuel à la surface
d'un cristal interagit avec ses plus proches voisins par l'intermédiaire
d'une distribution de forces dont la somme doit être nulle
pour respecter l'équilibre mécanique global du cristal.
Dans un développement multipolaire, la première contribution
à entrer en ligne de compte est alors un dipôle de forces.
De même, les marches sont des défauts linéaires sur la surface ;
à ce titre, elles sont le lieu d'une distribution linéaire
de dipôles de forces.
Tout comme en électromagnétisme,
l'énergie d'interaction
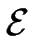 doublet
entre deux dipôles de force se comporte
comme 1/r3 en théorie de l'élasticité. Plus précisément
[#!Houchmandzadeh95!#] :
doublet
entre deux dipôles de force se comporte
comme 1/r3 en théorie de l'élasticité. Plus précisément
[#!Houchmandzadeh95!#] :
où E est le module d'Young et  , le coefficient de Poisson.
, le coefficient de Poisson.
 et
et
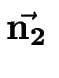 sont des vecteurs unitaires orientés selon les directions principales des dipôles (prises dans le plan de la surface, cf. réf.[#!Nozieres91!#]).
Deux marches vont alors interagir entre elles par l'intermédiaire de leur densités respectives de dipôles.
En ne considérant que les interactions élastiques entre marches voisines (ce qui constitue une bonne approximation [#!Ihle98!#]), la contribution élastique à l'énergie libre de la surface s'écrit :
sont des vecteurs unitaires orientés selon les directions principales des dipôles (prises dans le plan de la surface, cf. réf.[#!Nozieres91!#]).
Deux marches vont alors interagir entre elles par l'intermédiaire de leur densités respectives de dipôles.
En ne considérant que les interactions élastiques entre marches voisines (ce qui constitue une bonne approximation [#!Ihle98!#]), la contribution élastique à l'énergie libre de la surface s'écrit :
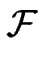 elas = elas = 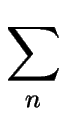   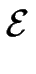 doublet( doublet(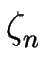 (xn), (xn),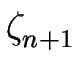 (xn + 1)) dsn dsn + 1 . (xn + 1)) dsn dsn + 1 .
|
(3.102) |
Dans le cas de deux marches droites, la seule longueur imposée par la géométrie est  .
L'énergie
.
L'énergie
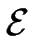 doublet
doublet  1/r3 intégrée une fois nous donne la densité d'énergie libre
1/r3 intégrée une fois nous donne la densité d'énergie libre
 1/
1/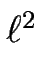 .
En général, le potentiel chimique local est calculé selon l'éq. [
.
En général, le potentiel chimique local est calculé selon l'éq. [![[*]](crossref.gif) ], puis introduit dans le modèle BCF via la relation de
Gibbs-Thomson [
], puis introduit dans le modèle BCF via la relation de
Gibbs-Thomson [![[*]](crossref.gif) ].
].
L'analyse de stabilité linéaire reste globalement inchangée par rapport au cas sans élasticité si ce n'est que cette dernière induit une renormalisation de la rigidité de ligne.
Le mode le plus instable est le mode en phase de longueur d'onde :
où 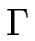 est défini par :
est défini par :
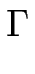 |
= |
   + +  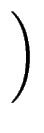 |
|
| |
= |
 (1 + Celas) . (1 + Celas) . |
(3.104) |
avec
Celas = 3A/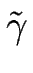
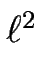 et
A = 2(1 -
et
A = 2(1 - 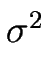 )(
)(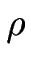 f )2/(
f )2/( E).
La rigidité de ligne est renormalisée par les interactions élastiques entre marches.
On peut, à l'aide d'un argument d'analyse dimensionnelle, donner l'ordre de grandeur de A et
E).
La rigidité de ligne est renormalisée par les interactions élastiques entre marches.
On peut, à l'aide d'un argument d'analyse dimensionnelle, donner l'ordre de grandeur de A et
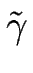 .
Dans la théorie continue de l'élasticité, il n'y a pas de longueur intrinsèque à part un « cut-off » microscopique a.
Ainsi, les seules grandeurs qui peuvent entrer en jeu dans l'ordre de grandeur de ces constantes sont le paramètre de maille a et le module d'Young E.
Dimensionnellement, on doit avoir
A
.
Dans la théorie continue de l'élasticité, il n'y a pas de longueur intrinsèque à part un « cut-off » microscopique a.
Ainsi, les seules grandeurs qui peuvent entrer en jeu dans l'ordre de grandeur de ces constantes sont le paramètre de maille a et le module d'Young E.
Dimensionnellement, on doit avoir
A  E a4 et
E a4 et
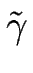
 E a2 ce qui indique que
Celas
E a2 ce qui indique que
Celas  (a/
(a/ )2
)2  1.
L'élasticité ne joue en général qu'un rôle négligeable dans le régime linéaire.
1.
L'élasticité ne joue en général qu'un rôle négligeable dans le régime linéaire.
Pour aborder l'étude non linéaire, nous nous restreignons au cas « en phase ».
Comme nous l'avons vu au paragraphe ![[*]](crossref.gif) , le comportement d'échelle du méandre
, le comportement d'échelle du méandre


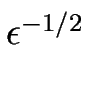 est singulier, et met enjeu des grandes variations
est singulier, et met enjeu des grandes variations
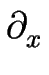

 1.
Les termes liés à l'élasticité n'influent pas sur le raisonnement du paragraphe
1.
Les termes liés à l'élasticité n'influent pas sur le raisonnement du paragraphe ![[*]](crossref.gif) ; les comportements d'échelles restent inchangés.
Le calcul du potentiel chimique (cf. éq.[
; les comportements d'échelles restent inchangés.
Le calcul du potentiel chimique (cf. éq.[![[*]](crossref.gif) ]) à partir de l'équation [
]) à partir de l'équation [![[*]](crossref.gif) ] conduit à :
] conduit à :
Cette expression a été calculée antérieurement par Bonzel et Mullins [#!Bonzel96!#] à partir d'une fonctionnelle d'énergie phénoménologique et macroscopique qui dépend de la densité de marches locale :
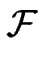 surf = surf =   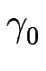 + +  | |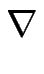 h| + h| + 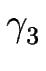 | |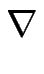 h|3 h|3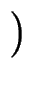 dS , dS ,
|
(3.106) |
où h est la hauteur de la surface, dS est un élément de surface et  ,
, 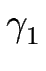 ,
,  sont des constantes.
Notre approche à partir de l'énergie d'interaction des marches permet non seulement un calcul général où les marches ne sont pas en phase mais aussi de relier les préfacteurs à des quantités microscopiques et de poursuivre le calcul aux ordres supérieurs.
sont des constantes.
Notre approche à partir de l'énergie d'interaction des marches permet non seulement un calcul général où les marches ne sont pas en phase mais aussi de relier les préfacteurs à des quantités microscopiques et de poursuivre le calcul aux ordres supérieurs.
L'analyse d'échelles multiples est analogue à celle du cas sans élasticité.
Nous obtenons une équation de la forme [![[*]](crossref.gif) ] où seul
] où seul  est différent.
Cette équation s'écrit sous forme normalisée :
est différent.
Cette équation s'écrit sous forme normalisée :
où 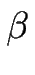 est défini comme précédemment par
est défini comme précédemment par
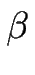 = DLa/DS
= DLa/DS .
.
Figure:
Évolution temporelle du méandre dans le cas de la diffusion de ligne (
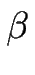 = +
= + 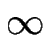 ) correspondant au dépôt de T = 1000) monocouches. La figure de gauche représente le cas sans élasticité (
Celas = 0) alors que celle de droite est un cas avec élasticité (
Celas = 0, 2).
) correspondant au dépôt de T = 1000) monocouches. La figure de gauche représente le cas sans élasticité (
Celas = 0) alors que celle de droite est un cas avec élasticité (
Celas = 0, 2).
|
|
Nous avons résolu numériquement l'équation [![[*]](crossref.gif) ] pour différentes valeurs de Celas et
] pour différentes valeurs de Celas et 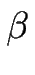 .
Dans tous les cas, une structure cellulaire apparaît et l'amplitude des cellules
croît avec le temps.
En présence d'élasticité (i.e. lorsque
Celas
.
Dans tous les cas, une structure cellulaire apparaît et l'amplitude des cellules
croît avec le temps.
En présence d'élasticité (i.e. lorsque
Celas  0),
les cellules coalescent et on observe que la taille latérale caractéristique des cellules croît dans le temps (cf fig. [
0),
les cellules coalescent et on observe que la taille latérale caractéristique des cellules croît dans le temps (cf fig. [![[*]](crossref.gif) ]).
]).
Les exposants de rugosité et de coarsening latéral peuvent être déterminés en cherchant les solutions self-similaires de l'équation [![[*]](crossref.gif) ] du méandre. Elles s'écrivent sous la forme :
] du méandre. Elles s'écrivent sous la forme :
où 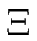 est l'exposant de rugosité et
est l'exposant de rugosité et  celui de mûrissement latéral du méandre. En injectant cette expression dans l'équation [
celui de mûrissement latéral du méandre. En injectant cette expression dans l'équation [![[*]](crossref.gif) ] et en écrivant que le terme de dérivé spatial
] et en écrivant que le terme de dérivé spatial
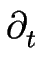
 , le terme déstabilisant ainsi que le terme stabilisant doivent avoir le même comportement d'échelle à temps long, on obtient deux équations qui permettent de déterminer les exposant
, le terme déstabilisant ainsi que le terme stabilisant doivent avoir le même comportement d'échelle à temps long, on obtient deux équations qui permettent de déterminer les exposant 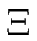 et
et  .
.
Les résultats sont les suivants :
- quelque soit le processus de relaxation envisagé, on a toujours
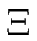 = 1/2 ; la prise en compte d'interactions élastiques entre marches n'a pas changé la croissance en t1/2 de l'amplitude du méandre.
= 1/2 ; la prise en compte d'interactions élastiques entre marches n'a pas changé la croissance en t1/2 de l'amplitude du méandre.
- en présence d'interactions élastiques, on trouve un exposant de mûrissement latéral
 non nul 3.9. En l'absence de diffusion de ligne (
non nul 3.9. En l'absence de diffusion de ligne (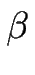 = 0), on trouve
= 0), on trouve
 = 1/6 alors que dès que celle-ci est présente on a
= 1/6 alors que dès que celle-ci est présente on a
 = 1/4.
= 1/4.
Ces résultats analytiques sont confirmés par les simulations numériques présentées figure [![[*]](crossref.gif) ].
].
Figure:
Les simulations ont été effectuées avec une constante élastique
Celas = 0, 2 pour différents processus de relaxation (i.e. différentes valeurs de 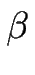 ).
).
a) Évolution au cours du temps de la rugosité W du méandre. Indépendamment du processus de relaxation, cette dernière suit, à temps long une loi de puissance en t0, 5.
b) Évolution temporelle de la longueur d'onde caractéristique 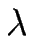 de la structure cellulaire du méandre. En l'absence de diffusion de ligne (
de la structure cellulaire du méandre. En l'absence de diffusion de ligne (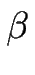 = 0), elle se comporte à temps long comme
t0, 17
= 0), elle se comporte à temps long comme
t0, 17  t1/6. Dès que la diffusion de ligne est présente, celle-ci domine dans le processus de « coarsening » et alors
t1/6. Dès que la diffusion de ligne est présente, celle-ci domine dans le processus de « coarsening » et alors
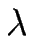
 t0, 25
t0, 25  t1/4.
t1/4.
| a) Rugosité |
b) Longueur d'onde caractéristique |
![\includegraphics[width=6cm,angle=-90]{../Images/scaling_law_rug_elas.eps}](img554.gif) |
|
|
Puisque
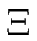 >
>  la distance locale entre les marches
la distance locale entre les marches


 /
/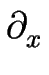

 t
t -
-  tend vers zéro avec le temps. En effet, en utilisant la forme « self-similaire » [
tend vers zéro avec le temps. En effet, en utilisant la forme « self-similaire » [![[*]](crossref.gif) ] du méandre, on a :
] du méandre, on a :
 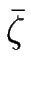 = t = t  f (X) f (X)  = t = t - -   f , f ,
|
(3.109) |
avec
X = x/t . Comme
. Comme
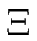 >
>  , on a, à temps long et dans les zones de forte pente (où
|
, on a, à temps long et dans les zones de forte pente (où
|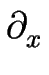
 |
|  1) :
1) :
Les interactions élastiques ne soignent pas le comportement du méandre qui voit se rapprocher inéluctablement les marches. Elles interviennent, malgré tout, positivement dans la dynamique. En effet, l'existence d'un mûrissement latéral de la structure ralentit le rapprochement des marches. Il reste cependant trop lent pour compenser complètement la croissance en t0, 5 de la rugosité.
Une analyse poussée des équations constitutives montre [#!Paulin01!#] qu'en fait, aucune répulsion dont l'énergie obéit à une loi de puissance
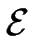
 1/
1/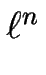 avec n > 1 (dans le cas de l'élasticité n=2) ne permet d'empêcher le resserrement des marches.
Seules des interactions à courte portée (par exemple de coeur dur ou exponentielles) pourraient limiter cet effet.
avec n > 1 (dans le cas de l'élasticité n=2) ne permet d'empêcher le resserrement des marches.
Seules des interactions à courte portée (par exemple de coeur dur ou exponentielles) pourraient limiter cet effet.
La surface semble ainsi vouloir développer une structure lamellaire dont la profondeur croît indéfiniment.
La robustesse de ce résultat en présence d'une répulsion entre les marches est surprenante.
L'étape suivante est naturellement de considérer un modèle réellement bidimensionnel, où les marches ne sont plus forcément en phase.
Des travaux dans ce sens sont en cours.
Présentons-en rapidement dans le paragraphe suivant quelques aspects préliminaires.




suivant: Méandre avec liberté de
monter: Méandre des marches en
précédent: Termes sous-dominants
Table des matières
fred
2001-07-02
![]() doublet
entre deux dipôles de force se comporte
comme 1/r3 en théorie de l'élasticité. Plus précisément
[#!Houchmandzadeh95!#] :
doublet
entre deux dipôles de force se comporte
comme 1/r3 en théorie de l'élasticité. Plus précisément
[#!Houchmandzadeh95!#] :
![[*]](crossref.gif) ], puis introduit dans le modèle BCF via la relation de
Gibbs-Thomson [
], puis introduit dans le modèle BCF via la relation de
Gibbs-Thomson [![[*]](crossref.gif) ].
].
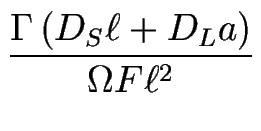
![[*]](crossref.gif) , le comportement d'échelle du méandre
, le comportement d'échelle du méandre
![]()
![]()
![]() est singulier, et met enjeu des grandes variations
est singulier, et met enjeu des grandes variations
![]()
![]()
![]() 1.
Les termes liés à l'élasticité n'influent pas sur le raisonnement du paragraphe
1.
Les termes liés à l'élasticité n'influent pas sur le raisonnement du paragraphe ![[*]](crossref.gif) ; les comportements d'échelles restent inchangés.
Le calcul du potentiel chimique (cf. éq.[
; les comportements d'échelles restent inchangés.
Le calcul du potentiel chimique (cf. éq.[![[*]](crossref.gif) ]) à partir de l'équation [
]) à partir de l'équation [![[*]](crossref.gif) ] conduit à :
] conduit à :
![[*]](crossref.gif) ] où seul
] où seul ![]() est différent.
Cette équation s'écrit sous forme normalisée :
est différent.
Cette équation s'écrit sous forme normalisée :
![[*]](crossref.gif) ] pour différentes valeurs de Celas et
] pour différentes valeurs de Celas et ![]() .
Dans tous les cas, une structure cellulaire apparaît et l'amplitude des cellules
croît avec le temps.
En présence d'élasticité (i.e. lorsque
Celas
.
Dans tous les cas, une structure cellulaire apparaît et l'amplitude des cellules
croît avec le temps.
En présence d'élasticité (i.e. lorsque
Celas ![]() 0),
les cellules coalescent et on observe que la taille latérale caractéristique des cellules croît dans le temps (cf fig. [
0),
les cellules coalescent et on observe que la taille latérale caractéristique des cellules croît dans le temps (cf fig. [![[*]](crossref.gif) ]).
]).
![[*]](crossref.gif) ] du méandre. Elles s'écrivent sous la forme :
] du méandre. Elles s'écrivent sous la forme :
![[*]](crossref.gif) ] et en écrivant que le terme de dérivé spatial
] et en écrivant que le terme de dérivé spatial
![[*]](crossref.gif) ].
].
![]() >
> ![]() la distance locale entre les marches
la distance locale entre les marches
![]()
![]()
![]() /
/![]()
![]()
![]() t
t![]() -
- ![]() tend vers zéro avec le temps. En effet, en utilisant la forme « self-similaire » [
tend vers zéro avec le temps. En effet, en utilisant la forme « self-similaire » [![[*]](crossref.gif) ] du méandre, on a :
] du méandre, on a :
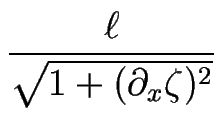
![]()
![]() 1/
1/![]() avec n > 1 (dans le cas de l'élasticité n=2) ne permet d'empêcher le resserrement des marches.
Seules des interactions à courte portée (par exemple de coeur dur ou exponentielles) pourraient limiter cet effet.
avec n > 1 (dans le cas de l'élasticité n=2) ne permet d'empêcher le resserrement des marches.
Seules des interactions à courte portée (par exemple de coeur dur ou exponentielles) pourraient limiter cet effet.