suivant: Cas bidimensionnel
monter: Différences finies
précédent: Différences finies
Table des matières
Cas unidimensionnel
Appelons h le pas constant du réseaux.
La méthode des différences finies consiste à discrétiser l'opérateur de différentiation donc à remplacer la dérivée d'ordre n d'une fonction f par l'évaluation de cette fonction sur m points :
f(n)(x)  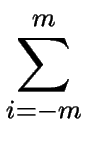 ai f (x + i h) . ai f (x + i h) .
|
(D.1) |
L'opérateur de différentiation discrétisé est donc défini par la donnée des coefficients ai.
La détermination de ces constantes est soumises à deux conditions.
La première est que l'opérateur de différentiation et son homologue discrétisé doivent se correspondre jusqu'à l'ordre désiré via les développements limités de f.
La seconde condition qui permet d'éviter des anisotropies numériques est que les deux opérateurs doivent avoir, dans la mesure du possible les mêmes symétries.
Prenons un cas simple : celui des dérivées première et seconde de f évaluées par un opérateur discrétisé sur 3 points.
Représentons ce dernier par :
|
= a f (x - h) + b f (x) + c f (x + h) .
|
(D.2) |
La fonction f peut être développée autour de x à l'aide d'un développement de Taylor :
f (x + n h) = f (x) + n h f'(x) + 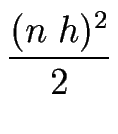 f''(x) + f''(x) +  f'''(x) + ... f'''(x) + ...
|
(D.3) |
Ce qui nous donne dans le cas présent :
|
= |
(a + b + c) f (x) + (c - a) h f'(x) + (c + a) f''(x) f''(x) |
|
| |
|
+ (c - a)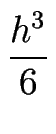 f'''(x) + (c + a) f'''(x) + (c + a)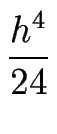 fIV(x) + O(h5) . fIV(x) + O(h5) . |
(D.4) |
Pour la dérivée première, l'opérateur doit être antisymétrique sous la transformation
x  - x, ce qui implique a = - c.
En faisant correspondre les développements de Taylor à la dérivée désirée, on a la condition supplémentaire
b = - (a + c) ; ce qui conduit à :
- x, ce qui implique a = - c.
En faisant correspondre les développements de Taylor à la dérivée désirée, on a la condition supplémentaire
b = - (a + c) ; ce qui conduit à :
f'(x) = 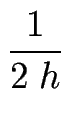 + O(h2) . + O(h2) .
|
(D.5) |
Pour la dérivée seconde, l'opérateur doit être symétrique par rapport à x, ce qui nous donne a = c et conduit à :
f''(x) =  + O(h2) . + O(h2) .
|
(D.6) |
L'approximation des précédentes dérivées à un ordre plus élevé implique de nouvelles contraintes ; il faut alors augmenter le nombre de paramètres ai, donc discrétiser l'opérateur sur un plus grand nombre de points. En imposant la symétrie
x  - x et la précision jusqu'à l'ordre h4, on détermine de façon unique l'opérateur de différentiation discrétisé (sur 5 points) correspondant à la dérivée seconde :
- x et la précision jusqu'à l'ordre h4, on détermine de façon unique l'opérateur de différentiation discrétisé (sur 5 points) correspondant à la dérivée seconde :
f''(x) = 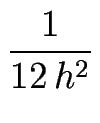 + O(h4) + O(h4)
|
(D.7) |
Pour les dérivées d'ordre supérieures une approche similaire conduit à :
f'''(x) = 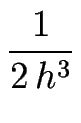 + O(h2) + O(h2)
|
(D.8) |
et
fIV(x) = 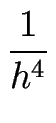 + O(h2) . + O(h2) .
|
(D.9) |
De même que précédemment, une précision supérieure nécessiterait une discrétisation sur un nombre plus important de points.




suivant: Cas bidimensionnel
monter: Différences finies
précédent: Différences finies
Table des matières
fred
2001-07-02
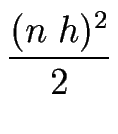 f''(x) +
f''(x) +  f'''(x) + ...
f'''(x) + ...