



suivant: Éléments finis
monter: Différences finies
précédent: Cas unidimensionnel
Table des matières
Cas bidimensionnel
À deux dimensions, la détermination des opérateurs de différences finies s'effectue de la même façon.
Cependant, le respect des symétries de l'opérateur de différentiation, peu important en dimension un devient ici crucial, leur non respect pouvant facilement entraîner des anisotropies numériques fortement préjudiciables à la consistance du schéma.
En dimension deux, bien que les différences finies imposent une grille régulière, on dispose d'une grande latitude pour le choix du type de réseau. Les réseaux carrés sont les plus communs mais d'autres types tels que des réseaux hexagonaux sont possibles. Ces derniers peuvent permettre de corriger un certain nombre d'anisotropies numériques mais sont plus difficiles à mettre en  uvre.
Pour la simulation de l'équation bidimensionnelle du méandre (chapitre
uvre.
Pour la simulation de l'équation bidimensionnelle du méandre (chapitre ![[*]](crossref.gif) ), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
|
= |
| |
| |
| A f (x + h, y) + B f (x - h, y) + C f (x, y + h) |
| + D f (x, y - h) + E f (x + h, y + h) + F f (x + h, y - h) |
| + G f (x - h, y + h) + H f (x - h, y - h) + I f (x, y) . |
|
|
Pour la dérivée partielle selon x, on impose à l'opérateur de différences finies l'antisymétrie par rapport à x et une invariance par transformation
y  - y ce qui se traduit par C = D = I = 0, A = - B et E = F = - G = - H et conduit à :
- y ce qui se traduit par C = D = I = 0, A = - B et E = F = - G = - H et conduit à :
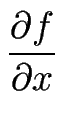 (x, y) = (x, y) = 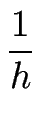
-E 0 E
-
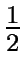 + 2E 0 + 2E 0
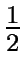 - 2 E
-E 0 E - 2 E
-E 0 E |
|
|
+ O(h2) .
|
(D.10) |
Avec E = 1/4, on retrouve la formule 25.3.22 de [#!Abramowitz70!#] et la formule 25.3.21 pour E = 0. Pour les simulations, nous avons choisi un schéma intermédiaire en prenant E = 1/8 :
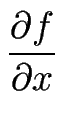 (x, y) = (x, y) = 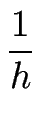
| -1/8 0 1/8
-1/4 0 1/4
-1/8 0 1/8 |
|
|
+ O(h2) ,
|
(D.11) |
et une expression similaire pour les dérivées dans la direction y :
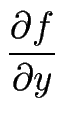 (x, y) = (x, y) = 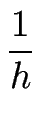
| 1/8 1/4 1/8
0 0 0
-1/8 -1/4 -1/8 |
|
|
+ O(h2) .
|
(D.12) |
Pour la dérivée partielle croisée
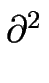 f /
f /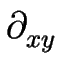 , on respecte l'antisymétrie de l'opérateur suivant x et y ; ce qui se traduit par E = - F = H = - G,
C = D = B = A = I = 0 et conduit à :
, on respecte l'antisymétrie de l'opérateur suivant x et y ; ce qui se traduit par E = - F = H = - G,
C = D = B = A = I = 0 et conduit à :
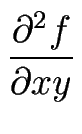 (x, y) = (x, y) = 
| -1/4 0 1/4
0 0 0
1/4 0 1/4 |
|
|
+ O(h2) ,
|
(D.13) |
ce qui est la formule 25.3.26 de [#!Abramowitz70!#].
Pour la dérivée partielle seconde suivant x, l'invariance de l'opérateur par rapport aux transformations
x  - x et
y
- x et
y  - y fournit les conditions suivantes : G = E = F = H, A = B et C = D et l'accord avec le développement de Taylor implique alors quant à lui : 2C + 4E = 0 et I = - 2A.
Ce qui conduit à l'expression suivante :
- y fournit les conditions suivantes : G = E = F = H, A = B et C = D et l'accord avec le développement de Taylor implique alors quant à lui : 2C + 4E = 0 et I = - 2A.
Ce qui conduit à l'expression suivante :
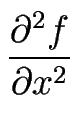 (x, y) = (x, y) = 
| E -2E E
1-2E 4E-2 1-2E
E -2E E |
|
|
+ O(h2) .
|
(D.14) |
Avec E = 0 (resp. E = 1/3) on retrouve l'expression 25.3.23 (resp. 25.3.25) de [#!Abramowitz70!#].
Nous avons choisi de prendre E = 1/8, ce qui permet de rendre le laplacien
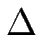 f =
f = 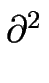 f /
f /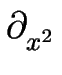 +
+ 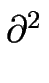 f /
f /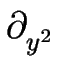 invariant D.1
par rotation de
45o et donne :
invariant D.1
par rotation de
45o et donne :
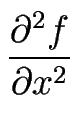 (x, y) = (x, y) = 
| 1/8 -1/4 1/8
3/4 -6/4 3/4
1/8 -1/4 1/8 |
|
|
+ O(h2) .
|
(D.15) |
Une expression similaire est obtenue pour la dérivée partielle seconde dans la direction y :
 (x, y) = (x, y) = 
| 1/8 3/4 1/8
-1/4 -6/4 -1/4
1/8 3/4 1/8 |
|
|
+ O(h2) .
|
(D.16) |




suivant: Éléments finis
monter: Différences finies
précédent: Cas unidimensionnel
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
![]() uvre.
Pour la simulation de l'équation bidimensionnelle du méandre (chapitre
uvre.
Pour la simulation de l'équation bidimensionnelle du méandre (chapitre ![[*]](crossref.gif) ), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
), nous avons fait le choix d'un réseau carré avec un pas h et d'une discrétisation des opérateurs différentiels sur 9 points. Utilisons la notation suivante pour la représentation des différents opérateurs de différences finies :
![]() - y ce qui se traduit par C = D = I = 0, A = - B et E = F = - G = - H et conduit à :
- y ce qui se traduit par C = D = I = 0, A = - B et E = F = - G = - H et conduit à :
![]() f /
f /![]() , on respecte l'antisymétrie de l'opérateur suivant x et y ; ce qui se traduit par E = - F = H = - G,
C = D = B = A = I = 0 et conduit à :
, on respecte l'antisymétrie de l'opérateur suivant x et y ; ce qui se traduit par E = - F = H = - G,
C = D = B = A = I = 0 et conduit à :
![]() - x et
y
- x et
y ![]() - y fournit les conditions suivantes : G = E = F = H, A = B et C = D et l'accord avec le développement de Taylor implique alors quant à lui : 2C + 4E = 0 et I = - 2A.
Ce qui conduit à l'expression suivante :
- y fournit les conditions suivantes : G = E = F = H, A = B et C = D et l'accord avec le développement de Taylor implique alors quant à lui : 2C + 4E = 0 et I = - 2A.
Ce qui conduit à l'expression suivante :