



suivant: Cas conservé
monter: Mise en paquets des
précédent: Mise en paquets des
Table des matières
Nous nous restreindrons dans ce qui suit au cas unidimensionnel : le méandre des marches sera négligé et on supposera alors que ces dernières restent parfaitement droites.
Nous considérerons le cas d'une surface vicinale soumise à un courant électrique continu perpendiculaire aux marches.
Les adatomes adsorbés sur les terrasses sont alors soumis à une force de la forme :
 = e zef = e zef  , ,
|
(4.1) |
appelée force d'électromigration, où e est la charge de l'électron,  est le champ électrique auquel est soumis l'adatome et zef est sa charge effective.
Cette force d'électromigration peut avoir deux origines distinctes. La première appelée force de vent est due au transfert de moment par friction des porteurs de charge du courant électrique sur le nuage électronique de l'adatome.
La charge effective zw < 0 correspondante peut être calculée à l'aide d'un modèle balistique [#!Fiks59!#], [#!Pierre-Louis97!#].
La deuxième origine de la force d'électromigration que nous appellerons force directe est l'interaction électrostatique entre le champ
est le champ électrique auquel est soumis l'adatome et zef est sa charge effective.
Cette force d'électromigration peut avoir deux origines distinctes. La première appelée force de vent est due au transfert de moment par friction des porteurs de charge du courant électrique sur le nuage électronique de l'adatome.
La charge effective zw < 0 correspondante peut être calculée à l'aide d'un modèle balistique [#!Fiks59!#], [#!Pierre-Louis97!#].
La deuxième origine de la force d'électromigration que nous appellerons force directe est l'interaction électrostatique entre le champ  et la distribution de charge de l'adatome.
Pour les métaux, la charge effective zd correspondante est tout simplement la charge ionique de l'adatome ; dans le cas général, elle tient compte des écrantages éventuels.
et la distribution de charge de l'adatome.
Pour les métaux, la charge effective zd correspondante est tout simplement la charge ionique de l'adatome ; dans le cas général, elle tient compte des écrantages éventuels.
La détermination de ces charges effectives et l'importance relative de chacune d'entre elle en fonction du régime de température considéré a fait l'objet de nombreuses recherches, aussi bien pour la force de vent [#!Fiks59!#], [#!Rous94!#] que la force d'électromigration directe [#!Bosvieux62!#], [#!Turban76!#] et reste encore à l'heure actuelle un sujet d'actualité [#!Fu97!#].
Nous nous contenterons ici d'une approche plus effective de l'électromigration et passerons sous silence l'origine exacte de la force d'électromigration
 . Les adatomes soumis à cette force que l'on considérera comme constante dérivent à la vitesse moyenne < V >, donnée par la relation d'Einstein :
. Les adatomes soumis à cette force que l'on considérera comme constante dérivent à la vitesse moyenne < V >, donnée par la relation d'Einstein :
< V > =  , ,
|
(4.2) |
où D est la constante de diffusion des adatomes sur la surface et Fel est prise positive pour une force d'électromigration descendant les marches.
On définit aussi couramment une longueur caractéristique d'électromigration :
 = =  . .
|
(4.3) |
La conséquence principale est l'apparition à la surface d'un flux de masse dû à l'électromigration :
|
J(z) = < V > c(z) ,
|
(4.4) |
où c est la concentration d'adatome sur les terrasses. Ce flux de masse induit par l'électromigration s'ajoute à celui apporté par la diffusion.
Examinons maintenant qualitativement l'effet de l'électromigration sur la stabilité du train de marches uniforme. Nous avons donc un ensemble de marches droites séparées par des terrasses de longueur  . Sur ces terrasses, la conservation de la masse, dans l'approximation quasi statique s'écrit pour la concentration c d'adatomes, en l'absence de désorption et d'adsorption :
. Sur ces terrasses, la conservation de la masse, dans l'approximation quasi statique s'écrit pour la concentration c d'adatomes, en l'absence de désorption et d'adsorption :
Cela signifie que le flux de masse
J =  - D
- D  c + (DFel/kBT) c
c + (DFel/kBT) c![$ \left.\vphantom{ -D \, \partial_z c + (DF_{el}/k_BT) \, c }\right]$](img660.gif) est constant sur les terrasses.
Considérons le cas où l'attachement des adatomes aux marches n'est pas instantané et appelons d la longueur Schwoebel : c'est la distance supplémentaire que parcourent les adatomes avant de pouvoir s'attacher aux marches 4.1. Elle est reliée au coefficient cinétique d'attachement
est constant sur les terrasses.
Considérons le cas où l'attachement des adatomes aux marches n'est pas instantané et appelons d la longueur Schwoebel : c'est la distance supplémentaire que parcourent les adatomes avant de pouvoir s'attacher aux marches 4.1. Elle est reliée au coefficient cinétique d'attachement 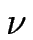 par d = D/
par d = D/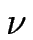 .
Soit ceq0, la concentration d'équilibre sur les terrasses ; si l'attachement est instantané (d = 0), le flux de masse est simplement
J = < V > ceq0.
Si tel n'est pas le cas (
d
.
Soit ceq0, la concentration d'équilibre sur les terrasses ; si l'attachement est instantané (d = 0), le flux de masse est simplement
J = < V > ceq0.
Si tel n'est pas le cas (
d 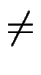 0), la longueur effective de la terrasse, que « voient » les adatomes n'est plus
0), la longueur effective de la terrasse, que « voient » les adatomes n'est plus  mais
mais
 + 2d ; il faut alors prendre en compte les longueurs cinétiques d'attachement.
Dans le cas où la force d'électromigration est suffisamment faible (
Fel
+ 2d ; il faut alors prendre en compte les longueurs cinétiques d'attachement.
Dans le cas où la force d'électromigration est suffisamment faible (
Fel  kBT/
kBT/ , autrement dit, si
, autrement dit, si


 ), la mobilité des adatomes, perpendiculairement aux marches,
est simplement modifiée par un facteur
), la mobilité des adatomes, perpendiculairement aux marches,
est simplement modifiée par un facteur
 /(
/( + 2d ) [#!Natori93!#], [#!Pierre-Louis97!#].
Le flux de matière sur une terrasse de longueur
+ 2d ) [#!Natori93!#], [#!Pierre-Louis97!#].
Le flux de matière sur une terrasse de longueur  dépend alors de la longueur de la terrasse :
J est une fonction strictement croissante de la taille des terrasses
dépend alors de la longueur de la terrasse :
J est une fonction strictement croissante de la taille des terrasses  .
Indexons les marches par m et notons
.
Indexons les marches par m et notons 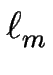 la longueur de la terrasse se trouvant devant la marche m. La vitesse de cette marche est donnée par une relation de conservation de la masse et prend la forme :
où
la longueur de la terrasse se trouvant devant la marche m. La vitesse de cette marche est donnée par une relation de conservation de la masse et prend la forme :
où 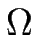 est la surface atomique dans le solide.
est la surface atomique dans le solide.
Imaginons maintenant une perturbation de la surface vicinale régulière par un déplacement de la marche m, comme illustré sur la figure [![[*]](crossref.gif) ].
].
Figure:
Vue schématique de l'instabilité de mise en paquets des marches induite par électromigration.
|
|
La terrasse m est alors plus étroite que ses voisines et d'après [![[*]](crossref.gif) ] :
] :
| Vm |
= |
  J( J( ) - J( ) - J(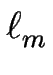 ) )![$\displaystyle \left.\vphantom{ J(\ell_{m-1}) - J(\ell_m) }\right]$](img668.gif) > 0 > 0 |
(4.8) |
| Vm + 1 |
= |
  J( J(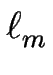 ) - J( ) - J( ) )![$\displaystyle \left.\vphantom{ J(\ell_m) - J(\ell_{m+1}) }\right]$](img672.gif) < 0 . < 0 . |
(4.9) |
La terrasse m voit alors sa taille diminuer dans le temps ; la perturbation initiale est donc amplifiée et le train de marche est instable vis-à-vis de l'appariement des marches.
De nombreuses études ont été consacrées à la mise en paquets des marches, que ce soit durant la sublimation de la surface vicinale, en présence d'effet Ehrlich-Schwoebel [#!Sato95b!#,#!Sato97!#] ou en présence d'électromigration [#!Misbah96!#] mais toutes restaient dans le cadre d'une désorption importante. Le résultat principal de ces études est que la densité
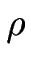 (z, t) de marches d'une surface vicinale souffrant d'une instabilité de mise en paquets, obéit dans ce cas à une équation de Benney :
(z, t) de marches d'une surface vicinale souffrant d'une instabilité de mise en paquets, obéit dans ce cas à une équation de Benney :
où a est fonction des paramètres physiques.
Pour la hauteur de la surface (reliée à la densité de marches par
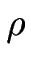 =
=  h), cette équation prend la forme :
h), cette équation prend la forme :
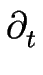 h = - h = -  h + a h + a  h - h - 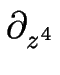 h + ( h + ( h)2 . h)2 .
|
(4.11) |
Cette équation conduit soit à du chaos spatio-temporel si a est petit (on retrouve alors la dynamique de l'équation de Kuramoto-Sivashinsky), soit à un arrangement régulier de cellules si a est grand (pour a très grand l'équation de Benney tend vers celle de Korteweg-de-Vries connue pour donner naissance à des solitons).
Dans les deux cas, la modulation de surface induite possède une longueur caractéristique qui n'évolue pas au cours du temps et aucun phénomène de mûrissement n'est observé.
Cependant, cette équation n'est valable que lorsque la désorption est suffisamment importante et plus précisément, lorsque la longueur de diffusion est plus petite que la longueur d'onde de la modulation.
Pour le cas du Silicium (1, 1, 1), il est bien connu que la longueur de diffusion est bien plus grande que la longueur caractéristique des modulations de surface dues à l'instabilité [#!Latyshev89!#].
Aux échelles de longueur qui nous intéressent, la dynamique est donc de nature conservée.
Il en découle alors immédiatement que l'équation de Benney ne peut décrire une telle dynamique ; en effet, elle ne s'écrit pas sous la forme d'une loi de conservation 4.2 (on verra plus loin que le préfacteur de la non-linéarité de l'équation de Benney s'annule en l'absence de désorption).
Dans la suite, nous montrons que la dynamique de l'instabilité de mise en paquets des marches suit, en l'absence de désorption, une équation de la forme :
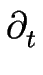 h = - h = -  h + a h + a h - h - 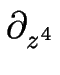 h + h +     h h ![$\displaystyle \left.\vphantom{ \left( \partial_z h \right)^2 }\right]$](img679.gif) . .
|
(4.12) |
Cette équation
conduit à une dynamique nouvelle : au lieu d'une structure régulière dérivant le long de la surface, un processus de mûrissement a lieu et la longueur d'onde caractéristique de la structure formée suit une loi de puissance de la forme
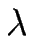
 t1/2, en accord avec de nombreuses observations expérimentales concernant le Silicium (1, 1, 1) [#!Yang96!#] pour lequel la longueur de diffusion est très grande.
t1/2, en accord avec de nombreuses observations expérimentales concernant le Silicium (1, 1, 1) [#!Yang96!#] pour lequel la longueur de diffusion est très grande.
Ce chapitre est consacré à la dérivation, à partir des équations discrètes du modèle de Burton-Cabrera-Frank, de l'équation d'évolution non linéaire appropriée pour la hauteur h(z, t) de la surface lorsque la longueur de désorption est grande.
Nous examinerons aussi le cas où la désorption est présente mais faible.
Cette étape nous permet de réaliser un pont entre les cas « conservé » et « non conservé » .
Il s'avèrera, et c'est là un point important,
que la limite de faible désorption est non triviale.
En particulier, on verra que ce n'est plus la non-linéarité
de Benney qui prévaut, mais d'autres non-linéarités
non rencontrées auparavant.
Nous montrerons que cela correspond à un régime dynamique intermédiaire entre le cas conservé (sans désorption) et celui donné par l'équation de Benney, lorsque la désorption est suffisamment importante.
Notre point de départ est le modèle de Burton, Cabrera et Frank [#!BCF51!#], dans lequel ont été inclus : la cinétique d'attachement [#!Schwoebel69!#] afin de rendre compte de l'écart à l'équilibre, l'interaction élastique entre marches, ainsi que la force d'électromigration Fel causée par un courant électrique (cf Fig. [![[*]](crossref.gif) ]).
Afin de simplifier l'étude, nous nous limiterons dans un premier temps au cas sans désorption (correspondant à une longueur de diffusion infinie : une fois adsorbés, les adatomes ne s'évaporent plus de la surface ; il y a conservation de la matière). Nous reviendrons sur ce point dans un paragraphe ultérieur.
]).
Afin de simplifier l'étude, nous nous limiterons dans un premier temps au cas sans désorption (correspondant à une longueur de diffusion infinie : une fois adsorbés, les adatomes ne s'évaporent plus de la surface ; il y a conservation de la matière). Nous reviendrons sur ce point dans un paragraphe ultérieur.




suivant: Cas conservé
monter: Mise en paquets des
précédent: Mise en paquets des
Table des matières
fred
2001-07-02
![]() . Les adatomes soumis à cette force que l'on considérera comme constante dérivent à la vitesse moyenne < V >, donnée par la relation d'Einstein :
. Les adatomes soumis à cette force que l'on considérera comme constante dérivent à la vitesse moyenne < V >, donnée par la relation d'Einstein :
 ,
,
![]() . Sur ces terrasses, la conservation de la masse, dans l'approximation quasi statique s'écrit pour la concentration c d'adatomes, en l'absence de désorption et d'adsorption :
. Sur ces terrasses, la conservation de la masse, dans l'approximation quasi statique s'écrit pour la concentration c d'adatomes, en l'absence de désorption et d'adsorption :

![[*]](crossref.gif) ].
].
![\includegraphics[width=10cm,angle=0]{../Images/bunching_hand.eps}](img669.gif)
![[*]](crossref.gif) ] :
] :
![]() (z, t) de marches d'une surface vicinale souffrant d'une instabilité de mise en paquets, obéit dans ce cas à une équation de Benney :
(z, t) de marches d'une surface vicinale souffrant d'une instabilité de mise en paquets, obéit dans ce cas à une équation de Benney :
![[*]](crossref.gif) ]).
Afin de simplifier l'étude, nous nous limiterons dans un premier temps au cas sans désorption (correspondant à une longueur de diffusion infinie : une fois adsorbés, les adatomes ne s'évaporent plus de la surface ; il y a conservation de la matière). Nous reviendrons sur ce point dans un paragraphe ultérieur.
]).
Afin de simplifier l'étude, nous nous limiterons dans un premier temps au cas sans désorption (correspondant à une longueur de diffusion infinie : une fois adsorbés, les adatomes ne s'évaporent plus de la surface ; il y a conservation de la matière). Nous reviendrons sur ce point dans un paragraphe ultérieur.