



suivant: Dynamique à l'ordre dominant
monter: Mise en paquets des
précédent: Force d'électromigration et mise
Table des matières
Cas conservé
La surface vicinale de désorientation  est soumise à un flux atomique incident F.
Les atomes atterrissent sur les terrasses de longueur
est soumise à un flux atomique incident F.
Les atomes atterrissent sur les terrasses de longueur  , y sont adsorbés et diffusent (avec une constante de diffusion D) avant de trouver un site d'attachement à la marche.
Sur une surface vicinale, les marches sont des sites privilégiés pour l'attachement des adatomes.
En s'attachant aux marches, ceux-ci les font avancer avec une vitesse V0 provoquant la croissance de la surface dans un régime dit « d'écoulement de marches » .
, y sont adsorbés et diffusent (avec une constante de diffusion D) avant de trouver un site d'attachement à la marche.
Sur une surface vicinale, les marches sont des sites privilégiés pour l'attachement des adatomes.
En s'attachant aux marches, ceux-ci les font avancer avec une vitesse V0 provoquant la croissance de la surface dans un régime dit « d'écoulement de marches » .
Figure:
Vue schématique de la surface vicinale montrant les notations utilisées dans le modèle.
|
|
Notons par c la concentration d'adatomes sur les terrasses. L'équation de diffusion des adatomes sur les terrasses, en présence d'électromigration
et dans l'approximation quasi statique prend la forme:
où nous rappelons que F est le flux atomique incident 4.3 et D la constante de diffusion sur les terrasses.
Fel est la force d'électromigration due au courant électrique agissant sur les adatomes et est définie positive dans le sens descendant les marches.
Aux marches, le flux de masse est relié à l'écart à l'équilibre thermodynamique par une relation « à la Onsager » :
| - Jm(zm) |
= |
 (cm(zm) - ceqm) , (cm(zm) - ceqm) , |
(4.14) |
| Jm(zm + 1) |
= |
 (cm(zm + 1) - ceqm + 1) . (cm(zm + 1) - ceqm + 1) . |
(4.15) |
zm est la position de la marche d'indice m et  sont des coefficients cinétiques d'attachement des adatomes aux marches ; ils ont la dimension d'une vitesse.
Un attachement impossible correspond à une valeur nulle de
sont des coefficients cinétiques d'attachement des adatomes aux marches ; ils ont la dimension d'une vitesse.
Un attachement impossible correspond à une valeur nulle de  alors qu'une cinétique instantanée est donnée par la limite
alors qu'une cinétique instantanée est donnée par la limite

 +
+ 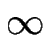 .
Les marches sont indexées par la variable m et ceqm est la concentration d'équilibre au bord de la marche m et tient compte des interactions élastiques entre marches [#!Pierre-Louis98a!#,#!Pierre-Louis98b!#,#!Pierre-Louis98c!#] ; pour une marche droite, celle-ci s'écrit :
.
Les marches sont indexées par la variable m et ceqm est la concentration d'équilibre au bord de la marche m et tient compte des interactions élastiques entre marches [#!Pierre-Louis98a!#,#!Pierre-Louis98b!#,#!Pierre-Louis98c!#] ; pour une marche droite, celle-ci s'écrit :
| ceqm |
= |
ceq0 1 + 1 +    - -   ![$\displaystyle \left.\vphantom{ 1 + {\cal A} \left( \frac{\ell^3}{\ell_m^3} - \frac{\ell^3}{\ell_{m-1}^3} \right) }\right]$](img690.gif) |
(4.16) |
| |
= |
ceq0 1 + 1 +  m m![$\displaystyle \left.\vphantom{ 1 + {\cal A}_m }\right]$](img692.gif) , , |
|
où ceq0 est la concentration d'équilibre au bord des marches pour des marches équidistantes sur la surface ;
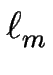 = zm + 1 - zm est la longueur de la terrasse m se trouvant devant la marche de même indice et
= zm + 1 - zm est la longueur de la terrasse m se trouvant devant la marche de même indice et  est relié à l'énergie élastique d'interaction entre marches par unité de longueur
est relié à l'énergie élastique d'interaction entre marches par unité de longueur
 par :
par :
 = =  , ,
|
(4.17) |
où 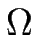 est l'aire atomique dans le solide.
Le courant de matière sur la terrasse m (pour
zm < z < zm + 1) est défini par :
est l'aire atomique dans le solide.
Le courant de matière sur la terrasse m (pour
zm < z < zm + 1) est défini par :
Jm(z) = -  D D  (z) - (z) -    cm(z) cm(z)![$\displaystyle \left.\vphantom{ D \, \frac{\partial c_m}{\partial z}(z) - \left( \frac{D F_{el}}{k_B T} \right) \, c_m(z) }\right]$](img697.gif) , ,
|
(4.18) |
ce qui inclut à la fois le courant de diffusion et celui dû à l'électromigration.
Finalement, la vitesse de la marche d'indice m est reliée aux courants de matière via une relation de conservation de la matière exprimée en z = zm :
Vm =   - Jm(zm) + Jm - 1(zm) - Jm(zm) + Jm - 1(zm)![$\displaystyle \left.\vphantom{ -J_m(z_m) + J_{m-1}(z_m) }\right]$](img699.gif) . .
|
(4.19) |
L'ensemble des équations [![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ] définit complètement la dynamique conservée des marches en présence d'électromigration.
] définit complètement la dynamique conservée des marches en présence d'électromigration.
Introduisons maintenant quelques variables adimensionnées.
Le temps sera redimensionné par 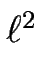 /D (t est remplacé par
tD/
/D (t est remplacé par
tD/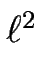 ) et les longueurs le long de z seront exprimées en unités de
) et les longueurs le long de z seront exprimées en unités de  , la longueur moyenne des terrasses.
Les concentrations seront redimensionnées par 1/
, la longueur moyenne des terrasses.
Les concentrations seront redimensionnées par 1/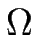 de sorte que dans ce qui suit c aura la signification d'un taux de couverture par rapport à la phase solide (où c = 1).
Le nombre de Péclet P est défini par
P = V0
de sorte que dans ce qui suit c aura la signification d'un taux de couverture par rapport à la phase solide (où c = 1).
Le nombre de Péclet P est défini par
P = V0  /D, où V0 est la vitesse stationnaire du train de marches équidistantes. Les coefficients cinétiques
/D, où V0 est la vitesse stationnaire du train de marches équidistantes. Les coefficients cinétiques  seront remplacés par
seront remplacés par

 /D =
/D =  /d± où d± est par définition la longueur Schwoebel.
On utilisera dans la suite
/d± où d± est par définition la longueur Schwoebel.
On utilisera dans la suite
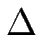
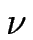 =
=  -
-  , qui caractérise l'effet Ehrlich-Schwoebel et
, qui caractérise l'effet Ehrlich-Schwoebel et
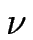 = (
= ( +
+  )/2.
Nous définissons aussi un coefficient d'électromigration adimensionné
R = Fel
)/2.
Nous définissons aussi un coefficient d'électromigration adimensionné
R = Fel /kB T =
/kB T =  /
/ . Dans les conditions expérimentales usuelles,
. Dans les conditions expérimentales usuelles,


 [#!Metois99!#] ; c'est à dire que R
[#!Metois99!#] ; c'est à dire que R  1.
1.
Lorsque les marches sont équidistantes,
la solution stationnaire pour la concentration d'adatomes
sur la terrasse m (pour
zm < z < zm + 1) s'écrit :
c0m(z) = A0eR(z - zm) + B0 +  (z - zm) , (z - zm) ,
|
(4.20) |
zm étant la position de la marche m et A0 et B0 des constantes d'intégration déterminées par les conditions limites [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ].
Le calcul de la vitesse V0 du train de marches équidistantes conduit à :
].
Le calcul de la vitesse V0 du train de marches équidistantes conduit à :
V0 =  F F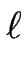 , ,
|
(4.21) |
ce qui est en accord avec la conservation globale de la matière.
L'analyse linéaire de stabilité du train de marches uniforme est accomplie en déterminant la réponse du train de marches à une perturbation de la forme :
zm = m + 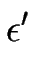 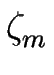 (t) . (t) .
|
(4.22) |
La perturbation
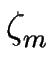 (t) est décomposée en modes de Fourier ; ceux-ci ne se couplant pas en régime linéaire, on peut étudier la réponse du train de marches à un mode :
(t) est décomposée en modes de Fourier ; ceux-ci ne se couplant pas en régime linéaire, on peut étudier la réponse du train de marches à un mode :
 étant le taux de croissance (ou atténuation) que nous souhaitons déterminer,
étant le taux de croissance (ou atténuation) que nous souhaitons déterminer, 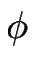 le déphasage entre marches adjacentes et
le déphasage entre marches adjacentes et 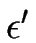 est un petit paramètre mesurant l'amplitude de la perturbation.
Cette perturbation du train de marches induit sur la terrasse m une perturbation du champ de concentration que l'on peut écrire :
est un petit paramètre mesurant l'amplitude de la perturbation.
Cette perturbation du train de marches induit sur la terrasse m une perturbation du champ de concentration que l'on peut écrire :
cm(z) = c0m(z) + 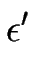 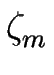 (t)c1m(z) , (t)c1m(z) ,
|
(4.24) |
où cm0(z) est la concentration pour le train de marches uniforme.
En insérant cette expression dans les équations du modèle, on détermine la réponse linéaire du système à une perturbation infinitésimale,
caractérisée par une relation de dispersion4.4 :
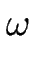 |
= |
C (2 sin(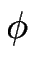 /2))2 - D (2 sin( /2))2 - D (2 sin(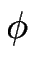 /2))4 /2))4 |
(4.25) |
| |
+ |
i P - P -   2 sin( 2 sin(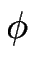 /2) /2)  sin( sin(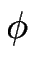 ) , ) , |
(4.26) |
avec
 |
= |
2 + +   , , |
(4.27) |
| C |
= |
  2 2  R ceq0 - P R ceq0 - P    , , |
(4.28) |
| D |
= |
 . . |
(4.29) |
La partie réelle de  représente le taux d'amplification de la perturbation au cours du temps.
Pour
représente le taux d'amplification de la perturbation au cours du temps.
Pour
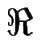 e(
e( ) > 0, la surface vicinale est instable vis-à-vis de l'instabilité de mise en paquets des marches.
Cela a lieu pour (cf. fig. [
) > 0, la surface vicinale est instable vis-à-vis de l'instabilité de mise en paquets des marches.
Cela a lieu pour (cf. fig. [![[*]](crossref.gif) ]) :
]) :
2   R ceq0 - P R ceq0 - P   > 0 . > 0 .
|
(4.30) |
L'instabilité se produit au delà d'une valeur critique de la force d'électromigration :
Rc =  . .
|
(4.31) |
Cette valeur critique du paramètre de contrôle qu'est la force d'électromigration, constitue un seuil pour l'instabilité. En deçà de ce seuil, le train de marche est stable alors qu'au-delà il souffre d'une instabilité de mise en paquets des marches.
Dans les conditions expérimentales usuelles,
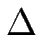
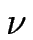 > 0, la surface vicinale est toujours instable pour une force d'électromigration positive R > Rc (c'est-à-dire une force d'électromigration descendant les marches).
La quantité qui fixe le taux de croissance :
2
> 0, la surface vicinale est toujours instable pour une force d'électromigration positive R > Rc (c'est-à-dire une force d'électromigration descendant les marches).
La quantité qui fixe le taux de croissance :
2 
 R ceq0 - P
R ceq0 - P 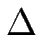
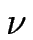 est petite dans les systèmes expérimentaux qui nous intéressent ; elle constitue le petit paramètre mesurant l'écart au seuil de l'instabilité dont nous nous servirons pour le développement de l'équation continue, sa faible valeur légitimera la limite continue.
Nous posons alors :
Le maximum de
est petite dans les systèmes expérimentaux qui nous intéressent ; elle constitue le petit paramètre mesurant l'écart au seuil de l'instabilité dont nous nous servirons pour le développement de l'équation continue, sa faible valeur légitimera la limite continue.
Nous posons alors :
Le maximum de
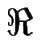 e(
e( ) est atteint pour une valeur
) est atteint pour une valeur  , le mode le plus instable (i.e. le mode instable ayant le taux de croissance le plus élevé).
À partir de l'équation [
, le mode le plus instable (i.e. le mode instable ayant le taux de croissance le plus élevé).
À partir de l'équation [![[*]](crossref.gif) ], nous obtenons les lois d'échelle suivantes :
Dans l'espace réel, cela signifie que nous avons des modulations de grande longueur d'onde évoluant lentement dans le temps. Plus précisément, l'évolution temporelle se produit sur des échelles de temps de l'ordre de
t
], nous obtenons les lois d'échelle suivantes :
Dans l'espace réel, cela signifie que nous avons des modulations de grande longueur d'onde évoluant lentement dans le temps. Plus précisément, l'évolution temporelle se produit sur des échelles de temps de l'ordre de
t 
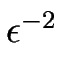 . La loi d'échelle de
. La loi d'échelle de 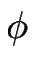 signifie que pour toute quantité fm dépendant de l'indice des marches m (par exemple la concentration cm), nous avons :
signifie que pour toute quantité fm dépendant de l'indice des marches m (par exemple la concentration cm), nous avons :
fm + 1 - fm = (ei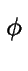 - 1)fm - 1)fm 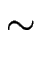 i i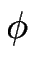 fm fm 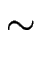 i i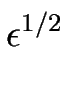 fm fm
|
(4.34) |
et en appelant 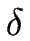 l'opérateur de différence finie :
l'opérateur de différence finie :
 fm = fm + 1 - fm fm = fm + 1 - fm 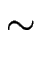 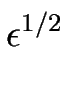 fm . fm .
|
(4.35) |
Une fois l'instabilité développée, les effets non linéaires deviennent importants.
Dans la suite, nous présenterons les grandes lignes de la dérivation de l'équation non linéaire d'évolution de l'instabilité.
Il nous a semblé commode d'extraire au préalable des conditions limites [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] la position des marches zm. À cet effet, nous effectuons le changement de variable suivant :
Z = (z - zm)/
] la position des marches zm. À cet effet, nous effectuons le changement de variable suivant :
Z = (z - zm)/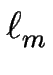 =
=  (z - zm), où
(z - zm), où
 = 1/
= 1/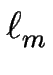 est la densité locale de marches.
Les équations constitutives du modèle [
est la densité locale de marches.
Les équations constitutives du modèle [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] se récrivent alors :
] se récrivent alors :
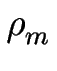  (0) - R cm(0) = (0) - R cm(0) =   cm(0) - ceqm cm(0) - ceqm , ,
|
(4.37) |
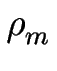  (1) - R cm(1) = - (1) - R cm(1) = -   cm(1) - ceqm + 1 cm(1) - ceqm + 1 , ,
|
(4.38) |
| Vm |
= |
 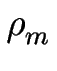  (0) - R cm(0) (0) - R cm(0)![$\displaystyle \left.\vphantom{ \rho_m \frac{\partial c_m}{\partial Z} (0) - R \;
c_m(0) }\right]$](img726.gif) - - 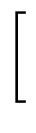   (1) - R cm - 1(1) (1) - R cm - 1(1)![$\displaystyle \left.\vphantom{ \rho_{m-1} \frac{\partial
c_{m-1}}{\partial Z}(1) - R \; c_{m-1}(1) }\right]$](img730.gif) . . |
(4.39) |
Comme R est petit dans les conditions expérimentales usuelles, il est
suffisant de se limiter à un développement au plus bas ordre en R pour la détermination du champ de concentration cm :
|
cm = cm0 + R cm1 + O(R2) .
|
(4.40) |
Les équations [![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ] nous permettent de déterminer cm :
] nous permettent de déterminer cm :
| cm(Z) |
= |
 - -  Z2 + am0Z + bm0 Z2 + am0Z + bm0![$\displaystyle \left.\vphantom{ -\frac{P \, \ell_m^2}{2} Z^2 + a_m^0 Z + b_m^0 }\right]$](img733.gif) |
|
| |
|
+ R  - -  Z3 + Z3 +  Z2 + am1Z + bm1 Z2 + am1Z + bm1![$\displaystyle \left.\vphantom{ -\frac{P \, \ell_m^3}{6} Z^3 + \frac{\ell_m \, a_m^0}{2} Z^2 + a_m^1 Z + b_m^1 }\right]$](img737.gif) + O(R2) + O(R2) |
(4.41) |
où
| am0 |
= |
 (ceqm + 1 - ceqm) + (ceqm + 1 - ceqm) +   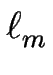 + +   , , |
(4.42) |
| bm0 |
= |
ceqm +   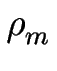  (ceqm + 1 - ceqm) + P + (ceqm + 1 - ceqm) + P +  ![$\displaystyle \left.\vphantom{ \rho_m \, \nu_- (c_{eq_{m+1}} - c_{eq_m} ) + P + \frac{\nu_- \, P \ell_m}{2} }\right]$](img746.gif) , , |
(4.43) |
| am1 |
= |
  ( ( + +  )bm0 + )bm0 +    - -    ![$\displaystyle \left.\vphantom{ (\nu_++\nu_-) b_m^0 + \nu_+\nu_- \frac{P\, \ell_m^3}{6} - \nu_+\nu_- \frac{\ell_m \, a_m^0}{2} }\right]$](img748.gif) , , |
(4.44) |
| bm1 |
= |
   - -  - bm0 - bm0![$\displaystyle \left.\vphantom{ \frac{P \, \ell_m^2}{6} - \frac{a_m^0}{2} - b_m^0 }\right]$](img753.gif) , , |
(4.45) |
où nous avons défini
 = 2
= 2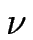 +
+ 

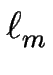 .
En utilisant l'équation [
.
En utilisant l'équation [![[*]](crossref.gif) ], nous trouvons que la vitesse de la marche m prend la forme :
], nous trouvons que la vitesse de la marche m prend la forme :
| Vm |
= |
P  + +     ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} }\right]$](img759.gif) - -      ceqm + ceqm - 1 ceqm + ceqm - 1 ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} \left( c_{eq_m}+c_{eq_{m-1}} \right) }\right]$](img764.gif) |
|
| |
+ |
    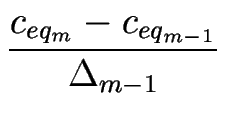 ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} \, \frac{c_{eq_m}-c_{eq_{m-1}}}{\Delta_{m-1}} }\right]$](img768.gif) + +     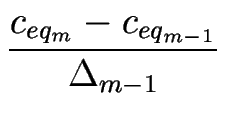 ![$\displaystyle \left.\vphantom{ \frac{c_{eq_m}-c_{eq_{m-1}}}{\Delta_{m-1}} }\right]$](img770.gif) |
|
| |
+ |
O(R2, PR) . |
(4.46) |
En utilisant la définition [![[*]](crossref.gif) ] de ceqm, on peut la reformuler comme suit afin de faire apparaître explicitement le paramètre
] de ceqm, on peut la reformuler comme suit afin de faire apparaître explicitement le paramètre
 = 2 R
= 2 R 
 ceq0 - P
ceq0 - P 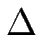
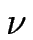 :
:
| Vm |
= |
P  - - ![$\displaystyle {\frac{\left[2 \, R \, \nu_+\nu_- \, c_{eq}^0 - P \, \Delta \nu\right]}{2}}$](img771.gif)    ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} }\right]$](img759.gif) |
|
| |
+ |
     ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} \, \frac{\delta {\cal A}_{m-1}}{\Delta_{m-1}} }\right]$](img775.gif) + +   ceq0 ceq0    ![$\displaystyle \left.\vphantom{ \frac{\delta {\cal A}_{m-1}}{\Delta_{m-1}} }\right]$](img777.gif) |
|
| |
- |
      m + m +  m - 1 m - 1 ![$\displaystyle \left.\vphantom{ \frac{\ell_{m-1}}{\Delta_{m-1}} \left( {\cal A}_m + {\cal A}_{m-1} \right) }\right]$](img782.gif) + O(R2, PR) . + O(R2, PR) . |
(4.47) |
Sous-sections




suivant: Dynamique à l'ordre dominant
monter: Mise en paquets des
précédent: Force d'électromigration et mise
Table des matières
fred
2001-07-02
![]() est soumise à un flux atomique incident F.
Les atomes atterrissent sur les terrasses de longueur
est soumise à un flux atomique incident F.
Les atomes atterrissent sur les terrasses de longueur ![]() , y sont adsorbés et diffusent (avec une constante de diffusion D) avant de trouver un site d'attachement à la marche.
Sur une surface vicinale, les marches sont des sites privilégiés pour l'attachement des adatomes.
En s'attachant aux marches, ceux-ci les font avancer avec une vitesse V0 provoquant la croissance de la surface dans un régime dit « d'écoulement de marches » .
, y sont adsorbés et diffusent (avec une constante de diffusion D) avant de trouver un site d'attachement à la marche.
Sur une surface vicinale, les marches sont des sites privilégiés pour l'attachement des adatomes.
En s'attachant aux marches, ceux-ci les font avancer avec une vitesse V0 provoquant la croissance de la surface dans un régime dit « d'écoulement de marches » .
 ,
,
![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ] définit complètement la dynamique conservée des marches en présence d'électromigration.
] définit complètement la dynamique conservée des marches en présence d'électromigration.
![]() /D (t est remplacé par
tD/
/D (t est remplacé par
tD/![]() ) et les longueurs le long de z seront exprimées en unités de
) et les longueurs le long de z seront exprimées en unités de ![]() , la longueur moyenne des terrasses.
Les concentrations seront redimensionnées par 1/
, la longueur moyenne des terrasses.
Les concentrations seront redimensionnées par 1/![]() de sorte que dans ce qui suit c aura la signification d'un taux de couverture par rapport à la phase solide (où c = 1).
Le nombre de Péclet P est défini par
P = V0
de sorte que dans ce qui suit c aura la signification d'un taux de couverture par rapport à la phase solide (où c = 1).
Le nombre de Péclet P est défini par
P = V0 ![]() /D, où V0 est la vitesse stationnaire du train de marches équidistantes. Les coefficients cinétiques
/D, où V0 est la vitesse stationnaire du train de marches équidistantes. Les coefficients cinétiques ![]() seront remplacés par
seront remplacés par
![]()
![]() /D =
/D = ![]() /d± où d± est par définition la longueur Schwoebel.
On utilisera dans la suite
/d± où d± est par définition la longueur Schwoebel.
On utilisera dans la suite
![]()
![]() =
= ![]() -
- ![]() , qui caractérise l'effet Ehrlich-Schwoebel et
, qui caractérise l'effet Ehrlich-Schwoebel et
![]() = (
= (![]() +
+ ![]() )/2.
Nous définissons aussi un coefficient d'électromigration adimensionné
R = Fel
)/2.
Nous définissons aussi un coefficient d'électromigration adimensionné
R = Fel![]() /kB T =
/kB T = ![]() /
/![]() . Dans les conditions expérimentales usuelles,
. Dans les conditions expérimentales usuelles,
![]()
![]()
![]() [#!Metois99!#] ; c'est à dire que R
[#!Metois99!#] ; c'est à dire que R ![]() 1.
1.
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ].
Le calcul de la vitesse V0 du train de marches équidistantes conduit à :
].
Le calcul de la vitesse V0 du train de marches équidistantes conduit à :
 .
.![[*]](crossref.gif) ]) :
L'instabilité se produit au delà d'une valeur critique de la force d'électromigration :
]) :
L'instabilité se produit au delà d'une valeur critique de la force d'électromigration :
 .
.
![[*]](crossref.gif) ], nous obtenons les lois d'échelle suivantes :
], nous obtenons les lois d'échelle suivantes :
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] la position des marches zm. À cet effet, nous effectuons le changement de variable suivant :
Z = (z - zm)/
] la position des marches zm. À cet effet, nous effectuons le changement de variable suivant :
Z = (z - zm)/![]() =
= ![]() (z - zm), où
(z - zm), où
![]() = 1/
= 1/![]() est la densité locale de marches.
Les équations constitutives du modèle [
est la densité locale de marches.
Les équations constitutives du modèle [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ], [
], [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] se récrivent alors :
] se récrivent alors :
![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ] nous permettent de déterminer cm :
] nous permettent de déterminer cm :
 Z2 + am1Z + bm1
Z2 + am1Z + bm1 (ceqm + 1 - ceqm) +
(ceqm + 1 - ceqm) + 




![[*]](crossref.gif) ], nous trouvons que la vitesse de la marche m prend la forme :
], nous trouvons que la vitesse de la marche m prend la forme :
![[*]](crossref.gif) ] de ceqm, on peut la reformuler comme suit afin de faire apparaître explicitement le paramètre
] de ceqm, on peut la reformuler comme suit afin de faire apparaître explicitement le paramètre
![]() = 2 R
= 2 R ![]()
![]() ceq0 - P
ceq0 - P ![]()
![]() :
: