


suivant: Limite continue
monter: Régime non linéaire
précédent: Régime non linéaire
Table des matières
Dans le but de rendre compte du régime non linéaire de la surface vicinale après que l'instabilité se soit développée, nous avons résolu numériquement l'ensemble des équations constitutives du modèle [![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ].
Contrairement au cas quasi statique pour lequel une équation fermée peut être obtenue pour la dynamique de la marche m en fonction de la position de ses voisines, les effets de retard induits par la relaxation de l'approximation quasi statique empêchent une telle possibilité.
Nous devons alors résoudre le problème complet dans le temps.
Ceci est réalisé par l'utilisation d'une fonction de Green appropriée.
Donnons ici les quelques lignes essentielles pour la compréhension de la méthode utilisée.
].
Contrairement au cas quasi statique pour lequel une équation fermée peut être obtenue pour la dynamique de la marche m en fonction de la position de ses voisines, les effets de retard induits par la relaxation de l'approximation quasi statique empêchent une telle possibilité.
Nous devons alors résoudre le problème complet dans le temps.
Ceci est réalisé par l'utilisation d'une fonction de Green appropriée.
Donnons ici les quelques lignes essentielles pour la compréhension de la méthode utilisée.
Le temps est, dans la suite adimensionné par
1/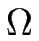 F, c'est-à-dire qu'il s'exprime en nombre de monocouches déposées. On pose
um(z) = cm(z) + z, ce qui nous permet de définir l'opérateur linéaire
F, c'est-à-dire qu'il s'exprime en nombre de monocouches déposées. On pose
um(z) = cm(z) + z, ce qui nous permet de définir l'opérateur linéaire  qui exprime l'équation de diffusion sur les terrasses :
qui exprime l'équation de diffusion sur les terrasses :
 um um |
= |
  + P + P  - P - P  ![$\displaystyle \left.\vphantom{\frac{\partial^2}{\partial z^2} + P \, \frac{\partial}{\partial z} - P \, \frac{\partial}{\partial t} }\right]$](img1090.gif) um um |
|
| |
= |
 + P + P  - P - P  |
|
| |
= |
0 |
(A.29) |
On définit l'opérateur de Green par :
 G( G( z, z, t) = - t) = -  ( ( z, z, t) , t) , |
|
|
(A.30) |
où
 z = z - z',
z = z - z',
 t = t - t' et
t = t - t' et
 est l'opérateur adjoint de
est l'opérateur adjoint de  au sens des distributions :
au sens des distributions :
Le calcul de G à partir de [![[*]](crossref.gif) ] nous donne :
] nous donne :
où H est la distribution de Heaviside et exprime la causalité de G.
L'opérateur de Green G va nous permettre de résoudre l'équation de diffusion [![[*]](crossref.gif) ] pour um sous la forme d'une équation intégrale.
On définit pour cela le domaine d'intégration
] pour um sous la forme d'une équation intégrale.
On définit pour cela le domaine d'intégration
 m0 par
m0 par
 m0 = [zm(t), zm + 1(t)]×[t0, t].
On évalue alors l'opérateur
m0 = [zm(t), zm + 1(t)]×[t0, t].
On évalue alors l'opérateur
 G appliqué à um sur
G appliqué à um sur
 m0 ; on a alorsA.5, en se servant de la définition de l'opérateur adjoint :
m0 ; on a alorsA.5, en se servant de la définition de l'opérateur adjoint :
  G( G( z, z, t) , um(z', t') t) , um(z', t')  |
= |
 G( G( z, z, t) , t) ,  um(z', t') um(z', t')  |
|
| |
|
+  F F  , , |
(A.33) |
où
 F
F  représente des termes intégrés sur le contour
représente des termes intégrés sur le contour

 m0 de
m0 de
 m0.
En faisant usage de ce que
m0.
En faisant usage de ce que
 um um |
= |
0 , |
(A.34) |
 G( G( z, z, t) t) |
= |
-  ( ( z, z, t) , t) , |
(A.35) |
on a
  ( ( z, z, t) , um(z', t') t) , um(z', t')  = - = -  F F  . . |
|
|
(A.36) |
L'évaluation de
 F
F  conduit alors à l'équation intégrale recherchée :
conduit alors à l'équation intégrale recherchée :
  ( ( z), um(z', t) z), um(z', t) ![$\displaystyle \rangle_{[z_m(t),z_{m+1}(t)]}^{}$](img1113.gif) |
= |
P  G( G( z, t - t0) um(z', t0) dz' z, t - t0) um(z', t0) dz' |
|
| |
|
+   G G  - um - um  - P,(1 + - P,(1 +  )G )G ![$\displaystyle \left.\vphantom{ G \,
\frac{\partial u_m}{\partial z'}
- u_m \lef...
... + \frac{\partial z'}{\partial t'} ) G \right) }\right]^{z_{m+1}(t')}_{z_m(t')}$](img1122.gif) dt' , dt' , |
|
| |
|
|
(A.37) |
où
  ( ( z), um(z', t) z), um(z', t) ![$\displaystyle \rangle_{[z_m(t),z_{m+1}(t)]}^{}$](img1113.gif) |
= |
  ( ( z)um(z', t) dz' z)um(z', t) dz' |
|
| |
= |
 (z) um(z) , (z) um(z) , |
|
avec
 (z) = 1 pour
z
(z) = 1 pour
z  ]zm, zm + 1[ et
]zm, zm + 1[ et
 (z) = 1/2 pour
z
(z) = 1/2 pour
z  {zm, zm + 1}.
Les gradients de concentration
{zm, zm + 1}.
Les gradients de concentration
 dans l'équation intégrale [
dans l'équation intégrale [![[*]](crossref.gif) ] sont exprimés, en fonction de um grâce aux équations cinétiques écrites en bord de terrasse.
] sont exprimés, en fonction de um grâce aux équations cinétiques écrites en bord de terrasse.
L'intégration des équations constitutives du modèle s'effectue alors comme suit. Pour chacune des terrasses, l'équation intégrale [![[*]](crossref.gif) ] permet de déterminer le champ de concentration non quasi statique. Connaissant le champ de concentration sur chacune des terrasses du train de marches, l'équation de continuité exprimant la conservation de la matière aux marches nous permet à chaque instant de déterminer la vitesse des marches.
] permet de déterminer le champ de concentration non quasi statique. Connaissant le champ de concentration sur chacune des terrasses du train de marches, l'équation de continuité exprimant la conservation de la matière aux marches nous permet à chaque instant de déterminer la vitesse des marches.
Figure:
Simulation numérique des équations [![[*]](crossref.gif) ]-[
]-[![[*]](crossref.gif) ] constitutives du modèle BCF pour un train de 300 marches,
à l'aide d'une fonction de Green spatio-temporelle. L'axe horizontal représente la position de chacune des marches du train de marches. L'axe vertical représente le temps, exprimé en nombre de monocouches déposées.
La condition initiale (à t = 0 est une perturbation aléatoire du train de marches).
] constitutives du modèle BCF pour un train de 300 marches,
à l'aide d'une fonction de Green spatio-temporelle. L'axe horizontal représente la position de chacune des marches du train de marches. L'axe vertical représente le temps, exprimé en nombre de monocouches déposées.
La condition initiale (à t = 0 est une perturbation aléatoire du train de marches).
|
|
Le résultat des simulations numériques est présenté sur la figure [![[*]](crossref.gif) ].
Comme cela était prévu par l'analyse linéaire, une instabilité se produit et les marches se regroupent en paquets.
Un peu plus loin dans le temps,
un processus de mûrissement peut être observé durant lequel les paquets de marches se regroupent.
Les paquets de marches interagissent entre eux soit par échange de marches entre deux paquets soit par absorption d'un petit paquet de marches par un plus gros.
].
Comme cela était prévu par l'analyse linéaire, une instabilité se produit et les marches se regroupent en paquets.
Un peu plus loin dans le temps,
un processus de mûrissement peut être observé durant lequel les paquets de marches se regroupent.
Les paquets de marches interagissent entre eux soit par échange de marches entre deux paquets soit par absorption d'un petit paquet de marches par un plus gros.
Connaissant à chaque instant la position relative de chacune des marches au sein du train de marches, nous pouvons reconstituer le profil de la surface vicinale ; une telle reconstruction de la surface vicinale est présentée sur la figure [![[*]](crossref.gif) ].
].
On observe, sur la surface, la formation d'une structure cellulaire. Chacune de ces cellules étant la trace d'un paquet de marches. Le profil de la surface subit un processus de mûrissement au cours duquel la longueur d'onde caractéristique de la structure cellulaire formée évolue au cours du temps comme
t , avec
, avec

 0, 5. Sur la figure [
0, 5. Sur la figure [![[*]](crossref.gif) ] nous présentons l'évolution au cours du temps de la longueur d'onde caractéristique de la structure cellulaire du profil de la surface vicinale.
] nous présentons l'évolution au cours du temps de la longueur d'onde caractéristique de la structure cellulaire du profil de la surface vicinale.
Figure:
À partir de la simulation (voir fig. [![[*]](crossref.gif) ]) discrète du train de marches, nous avons reconstitué le profil de la surface vicinale. La figure représente le profil de la surface à laquelle la pente moyenne a été retranchée. Les points noirs sur la courbe supérieure représentent la position des marches sur la surface.
]) discrète du train de marches, nous avons reconstitué le profil de la surface vicinale. La figure représente le profil de la surface à laquelle la pente moyenne a été retranchée. Les points noirs sur la courbe supérieure représentent la position des marches sur la surface.
|
|
Figure:
Loi de mûrissement obtenue à partir des simulations discrètes du train de marches. L'axe vertical représente la longueur d'onde caractéristique de la surface et l'axe horizontal, le temps t.
 |



suivant: Limite continue
monter: Régime non linéaire
précédent: Régime non linéaire
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ] à [
] à [![[*]](crossref.gif) ].
Contrairement au cas quasi statique pour lequel une équation fermée peut être obtenue pour la dynamique de la marche m en fonction de la position de ses voisines, les effets de retard induits par la relaxation de l'approximation quasi statique empêchent une telle possibilité.
Nous devons alors résoudre le problème complet dans le temps.
Ceci est réalisé par l'utilisation d'une fonction de Green appropriée.
Donnons ici les quelques lignes essentielles pour la compréhension de la méthode utilisée.
].
Contrairement au cas quasi statique pour lequel une équation fermée peut être obtenue pour la dynamique de la marche m en fonction de la position de ses voisines, les effets de retard induits par la relaxation de l'approximation quasi statique empêchent une telle possibilité.
Nous devons alors résoudre le problème complet dans le temps.
Ceci est réalisé par l'utilisation d'une fonction de Green appropriée.
Donnons ici les quelques lignes essentielles pour la compréhension de la méthode utilisée.
 + P
+ P 
 e-
e-  G(
G(![$\displaystyle \left.\vphantom{ G \,
\frac{\partial u_m}{\partial z'}
- u_m \lef...
... + \frac{\partial z'}{\partial t'} ) G \right) }\right]^{z_{m+1}(t')}_{z_m(t')}$](img1122.gif) dt' ,
dt' ,