



suivant: Analyse linéaire de stabilité
monter: Régime non linéaire
précédent: Formalisme de Green et
Table des matières
Résoudre l'ensemble des équations intégrales pour le train de marches est très coûteux aussi bien en ressources numériques qu'en temps de calcul et ne donne pas une image totalement satisfaisante de la dynamique.
Une image continue de la dynamique porte plus de promesses.
Il serait alors intéressant d'extraire des équations constitutives du modèle une équation non linéaire permettant de décrire de façon pertinente la dynamique du profil de la surface vicinale.
C'est ce que nous nous proposons d'aborder maintenant.
Le déroulement des calculs ayant conduit à l'équation d'évolution non linéaire du profil de la surface est similaire à celui détaillé au chapitre ![[*]](crossref.gif) ; donnons-en ici les principales étapes.
Nous nous placerons dans l'approximation quasi statique (c'est-à-dire que les termes d'ordre P2 et supérieur seront négligés) mais nous conserverons les termes relatifs à l'advection.
Nous considérerons aussi un faible effet Ehrlich-Schwoebel :
; donnons-en ici les principales étapes.
Nous nous placerons dans l'approximation quasi statique (c'est-à-dire que les termes d'ordre P2 et supérieur seront négligés) mais nous conserverons les termes relatifs à l'advection.
Nous considérerons aussi un faible effet Ehrlich-Schwoebel :
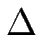
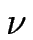
 1.
À partir de la relation de dispersion [
1.
À partir de la relation de dispersion [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) -
- ![[*]](crossref.gif) ] développée jusqu'à l'ordre P, nous identifions le seuil de l'instabilité ainsi qu'un paramètre de contrôle
] développée jusqu'à l'ordre P, nous identifions le seuil de l'instabilité ainsi qu'un paramètre de contrôle
 = (4
= (4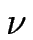 ceq0 -
ceq0 - 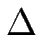
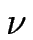 )/(2
)/(2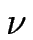 +
+  ) qui mesurera l'écart par rapport à ce seuil.
Pour
) qui mesurera l'écart par rapport à ce seuil.
Pour
 < 0, le train de marches est stable vis-à-vis de l'instabilité de mise en paquets des marches alors que pour
< 0, le train de marches est stable vis-à-vis de l'instabilité de mise en paquets des marches alors que pour
 > 0, l'instabilité de mise en paquets des marches se manifeste.
Nous nous plaçons proche du seuil de l'instabilité de telle sorte que
> 0, l'instabilité de mise en paquets des marches se manifeste.
Nous nous plaçons proche du seuil de l'instabilité de telle sorte que

 1.
L'examen de la relation de dispersion nous permet d'identifier les échelles de temps et d'espace caractéristiques de la dynamique.
Dans l'espace de Fourier, nous obtenons
1.
L'examen de la relation de dispersion nous permet d'identifier les échelles de temps et d'espace caractéristiques de la dynamique.
Dans l'espace de Fourier, nous obtenons



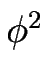 -
-  + i
+ i où la partie imaginaire, linéaire en
où la partie imaginaire, linéaire en 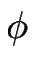 a été absorbée au moyen d'une transformation galiléenne
m
a été absorbée au moyen d'une transformation galiléenne
m  m + t.
Nous pouvons voir que
m + t.
Nous pouvons voir que 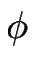 se comporte comme
se comporte comme
 .
La partie imaginaire de
.
La partie imaginaire de  se comporte alors comme
se comporte alors comme
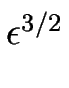 alors que la partie réelle se comporte comme
alors que la partie réelle se comporte comme
 .
Cela signifie que dans un développement multi-échelle, nous devons introduire un temps court associé à la propagation de la perturbation et un temps long associé à sa croissance.
Alors, nous introduisons un temps redimensionné
T = Ti + Tr =
.
Cela signifie que dans un développement multi-échelle, nous devons introduire un temps court associé à la propagation de la perturbation et un temps long associé à sa croissance.
Alors, nous introduisons un temps redimensionné
T = Ti + Tr = 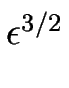 t +
t +  t et nous redimensionnons de même l'indice des marches
M =
t et nous redimensionnons de même l'indice des marches
M =  m (m peut être considéré comme une variable continue car la hauteur de la surface s'écrit h = - m a où a est une distance atomique).
Alors
zm(t) = z(m, t)
m (m peut être considéré comme une variable continue car la hauteur de la surface s'écrit h = - m a où a est une distance atomique).
Alors
zm(t) = z(m, t)  z(h, t).
À l'ordre P, l'approximation quasi statique est valable et alors, nous pouvons exprimer la vitesse de la marche m explicitement en fonction de la position et de la vitesse des marches voisines :
z(h, t).
À l'ordre P, l'approximation quasi statique est valable et alors, nous pouvons exprimer la vitesse de la marche m explicitement en fonction de la position et de la vitesse des marches voisines :
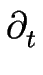 zm = F(zm, zm + 1, zm - 1, zm = F(zm, zm + 1, zm - 1,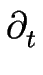 zm + 1, zm + 1,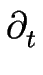 zm - 1) . zm - 1) .
|
(A.38) |
Nous définissons
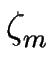 (t) = zm(t) - m, l'écart de position de la marche m par rapport à sa position dans le train de marches uniforme. Il doit être développé en échelle de
(t) = zm(t) - m, l'écart de position de la marche m par rapport à sa position dans le train de marches uniforme. Il doit être développé en échelle de
 :
:
 =
=  (Z(0) +
(Z(0) + 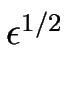 Z(1/2) +
Z(1/2) +  Z(1) +
Z(1) + 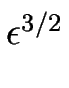 Z(3/2) + ... ).
L'exposant
Z(3/2) + ... ).
L'exposant  est déterminé par la condition que les termes non linéaires dominants doivent être du même ordre en
est déterminé par la condition que les termes non linéaires dominants doivent être du même ordre en  que les termes linéaires ; dans le cas présent, nous trouvons
que les termes linéaires ; dans le cas présent, nous trouvons  = 0 i.e.
= 0 i.e.

 Z0 + ...
Z0 + ...  O(
O( ).
Le développement multi-échelle peut alors être effectué en développant l'équation
[
).
Le développement multi-échelle peut alors être effectué en développant l'équation
[![[*]](crossref.gif) ] jusqu'à l'ordre
] jusqu'à l'ordre
 .
Nous obtenons alors une équation non linéaire pour la position
.
Nous obtenons alors une équation non linéaire pour la position 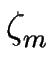 des marches.
De la même manière qu'au chapitre
des marches.
De la même manière qu'au chapitre ![[*]](crossref.gif) , nous pouvons la traduire en une équation continue pour le profil de la surface vicinale.
Cette dernière s'écrit :
, nous pouvons la traduire en une équation continue pour le profil de la surface vicinale.
Cette dernière s'écrit :
 |
= |
- a2  + a3 + a3  - a4 - a4  + aNL + aNL      ![$\displaystyle \left.\vphantom{ \left( \frac{\partial H}{\partial Z} \right)^2 }\right]$](img1145.gif) , , |
|
| |
|
|
(A.39) |
où H est la hauteur de la surface à laquelle la pente moyenne a été retranchée.
On a défini :
| a2 |
= |
   4 4 ceq0 - ceq0 -   ![$\displaystyle \left.\vphantom{ \frac{}{} 4 \nu c_{eq}^0 - \Delta \nu }\right]$](img1148.gif) , , |
|
| a3 |
= |
 + +  , , |
|
| a4 |
= |
 + +  , , |
|
| aNL |
= |
   + +  ![$\displaystyle \left.\vphantom{ \frac{1}{6} + \frac{21 \, \nu_+ \nu_- \, {\cal A} c_{eq}^0}{2(2\nu + \nu^2)} }\right]$](img1155.gif) . . |
(A.40) |
Cette équation est générique (cf annexe ![[*]](crossref.gif) ) ; elle a été rencontrée récemment [#!Csahok00!#] dans le contexte de l'étude de la formation des rides sur le sable ; nous l'avons aussi rencontrée lors de l'étude de la mise en paquets des marches induite par un courant d'électromigration.
Le fait que le flux apparaît (via le nombre de Péclet P) dans le coefficient du terme non linéaire aNL n'est pas une surprise car le terme non linéaire n'est pas variationnel et ne peut être induit que par des effet hors équilibre (il doit donc disparaître à l'équilibre).
) ; elle a été rencontrée récemment [#!Csahok00!#] dans le contexte de l'étude de la formation des rides sur le sable ; nous l'avons aussi rencontrée lors de l'étude de la mise en paquets des marches induite par un courant d'électromigration.
Le fait que le flux apparaît (via le nombre de Péclet P) dans le coefficient du terme non linéaire aNL n'est pas une surprise car le terme non linéaire n'est pas variationnel et ne peut être induit que par des effet hors équilibre (il doit donc disparaître à l'équilibre).
Figure:
Simulation numérique de l'équation [![[*]](crossref.gif) ], en partant d'un front initialement perturbé aléatoirement. La taille du système est de dix fois la longueur d'onde la plus instable. L'évolution temporelle montre un mûrissement de la structure formée.
], en partant d'un front initialement perturbé aléatoirement. La taille du système est de dix fois la longueur d'onde la plus instable. L'évolution temporelle montre un mûrissement de la structure formée.
|
|
Un
point important est que l'équation [![[*]](crossref.gif) ] conduit à un mûrissement de la struture formée (voir fig.[
] conduit à un mûrissement de la struture formée (voir fig.[![[*]](crossref.gif) ] pour une intégration numérique de l'équation [
] pour une intégration numérique de l'équation [![[*]](crossref.gif) ] ).
Le comportement du modèle continu est en très bon accord avec l'intégration numérique complète du modéle BCF (voir fig.[
] ).
Le comportement du modèle continu est en très bon accord avec l'intégration numérique complète du modéle BCF (voir fig.[![[*]](crossref.gif) ]).
Les deux images sont qualitativement semblables et présentent de fortes similitude pour le comportement du profil de la surface. De plus les lois d'échelle pour le comportement de la longueur caractéristique de la structure sont en bon accord qualitatif (voir figures [
]).
Les deux images sont qualitativement semblables et présentent de fortes similitude pour le comportement du profil de la surface. De plus les lois d'échelle pour le comportement de la longueur caractéristique de la structure sont en bon accord qualitatif (voir figures [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]).
L'équation [
]).
L'équation [![[*]](crossref.gif) ] est donc bien l'équation pertinente qui permet de rendre compte de l'instabilité de mise en paquets des marches induite par advection.
] est donc bien l'équation pertinente qui permet de rendre compte de l'instabilité de mise en paquets des marches induite par advection.
Figure:
Loi de mûrissement obtenue à partir des simulations numériques de l'équation [![[*]](crossref.gif) ].
].
 |




suivant: Analyse linéaire de stabilité
monter: Régime non linéaire
précédent: Formalisme de Green et
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ; donnons-en ici les principales étapes.
Nous nous placerons dans l'approximation quasi statique (c'est-à-dire que les termes d'ordre P2 et supérieur seront négligés) mais nous conserverons les termes relatifs à l'advection.
Nous considérerons aussi un faible effet Ehrlich-Schwoebel :
; donnons-en ici les principales étapes.
Nous nous placerons dans l'approximation quasi statique (c'est-à-dire que les termes d'ordre P2 et supérieur seront négligés) mais nous conserverons les termes relatifs à l'advection.
Nous considérerons aussi un faible effet Ehrlich-Schwoebel :
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) -
- ![[*]](crossref.gif) ] développée jusqu'à l'ordre P, nous identifions le seuil de l'instabilité ainsi qu'un paramètre de contrôle
] développée jusqu'à l'ordre P, nous identifions le seuil de l'instabilité ainsi qu'un paramètre de contrôle 
 ,
, +
+  ,
,