next up previous contents
suivant: Cas général : avec monter: Cas en phase précédent: Ordre dominant   Table des matières

Termes sous-dominants

Le développement peut être poursuivi aux ordres supérieurs. Donnons la poursuite du calcul pour les termes sous-dominants.

Ordre 3/2

À partir de l'équation [[*]], nous trouvons que U(3/2) obéit à l'équation suivante :

$\displaystyle \cal {H}$(0) $\displaystyle \partial_{\cal ZZ}^{}$U(3/2) + $\displaystyle \cal {H}$(1/2) $\displaystyle \partial_{\cal ZZ}^{}$U(1) + $\displaystyle \cal {H}$(1) $\displaystyle \partial_{\cal ZZ}^{}$U(1/2)      
-2 $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{{\cal Z}X}^{}$U(1) - 2 $\displaystyle \partial_{X}^{}$H(1/2) $\displaystyle \partial_{{\cal Z}X}^{}$U(1/2)      
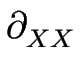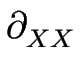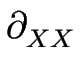- $\displaystyle \partial_{XX}^{}$H(0) $\displaystyle \partial_{\cal Z}^{}$U(1) - $\displaystyle \partial_{XX}^{}$H(1/2) $\displaystyle \partial_{\cal Z}^{}$U(1/2) + $\displaystyle \partial_{XX}^{}$U(1/2) = 0  . (C.34)

dont la solution générale prend la forme (en se servant des expressions de U(1) et U(1/2)) :

U(3/2) = $\displaystyle {\frac{a^{(3/2)}}{12}}$$\displaystyle \cal {Z}$4 + $\displaystyle {\frac{b^{(3/2)}}{6}}$$\displaystyle \cal {Z}$3 + $\displaystyle {\frac{c^{(3/2)}}{2}}$$\displaystyle \cal {Z}$2 + A(3/2)$\displaystyle \cal {Z}$  , (C.35)

avec
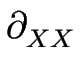a(3/2) = $\displaystyle {\frac{1}{{\cal H}^{(0)}}}$ $\displaystyle \left[\vphantom{ \frac{}{} \partial_X H^{(0)} \, \partial_X b^{(1... 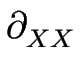...ac{1}{2} \, \partial_{XX} H^{(0)} \, b^{(1)} - \partial_{XX} a^{(1/2)} }\right.$$\displaystyle {\frac{}{}}$$\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{X}^{}$b(1) + $\displaystyle {\textstyle\frac{1}{2}}$ $\displaystyle \partial_{XX}^{}$H(0) b(1) - $\displaystyle \partial_{XX}^{}$a(1/2)$\displaystyle \left.\vphantom{ \frac{}{} \partial_X H^{(0)} \, \partial_X b^{(1... ...ac{1}{2} \, \partial_{XX} H^{(0)} \, b^{(1)} - \partial_{XX} a^{(1/2)} }\right]$  ,  
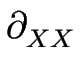b(3/2) = $\displaystyle {\frac{1}{{\cal H}^{(0)}}}$ $\displaystyle \left[\vphantom{ \frac{}{} 2 \, \partial_X H^{(0)} \, \partial_X a^{(1)} - {\cal H}^{1/2} \, b^{(1)} + \partial_{XX} H^{(0)} \, a^{(1)} }\right.$$\displaystyle {\frac{}{}}$2 $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{X}^{}$a(1) - $\displaystyle \cal {H}$1/2 b(1) + $\displaystyle \partial_{XX}^{}$H(0) a(1)  
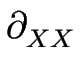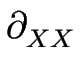    $\displaystyle \left.\vphantom{ \frac{}{} + 4 \, \partial_X a^{(1/2)} \, \partia... ... + 2 \, a^{(1/2)} \, \partial_{XX} H^{(1/2)} - \partial_{XX} A^{(1/2)} }\right.$$\displaystyle {\frac{}{}}$ + 4 $\displaystyle \partial_{X}^{}$a(1/2) $\displaystyle \partial_{X}^{}$H(1/2) + 2 a(1/2) $\displaystyle \partial_{XX}^{}$H(1/2) - $\displaystyle \partial_{XX}^{}$A(1/2)$\displaystyle \left.\vphantom{ \frac{}{} + 4 \, \partial_X a^{(1/2)} \, \partia... ... + 2 \, a^{(1/2)} \, \partial_{XX} H^{(1/2)} - \partial_{XX} A^{(1/2)} }\right]$  ,  
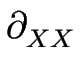c(3/2) = $\displaystyle {\frac{1}{{\cal H}^{(0)}}}$ $\displaystyle \left[\vphantom{ \frac{}{} - {\cal H}^{(1/2)} \, a^{(1)} + 2 \, \... ...ial_X H^{(0)} \, \partial_X A^{(1)} + \partial_{XX} H^{(0)} \, A^{(1)} }\right.$$\displaystyle {\frac{}{}}$ - $\displaystyle \cal {H}$(1/2) a(1) + 2 $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{X}^{}$A(1) + $\displaystyle \partial_{XX}^{}$H(0) A(1)  
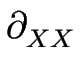    $\displaystyle \left.\vphantom{ \frac{}{} - 2 \, a^{(1/2)} \, {\cal H}^{(1)} + 2... ...{(1/2)} \, \partial_X A^{(1/2)} + \partial_{XX} H^{(1/2)} \, A^{(1/2)} }\right.$$\displaystyle {\frac{}{}}$ - 2 a(1/2) $\displaystyle \cal {H}$(1) + 2 $\displaystyle \partial_{X}^{}$H(1/2) $\displaystyle \partial_{X}^{}$A(1/2) + $\displaystyle \partial_{XX}^{}$H(1/2) A(1/2)  
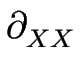    $\displaystyle \left.\vphantom{ \frac{}{} - \partial_{XX} B^{(1/2)} }\right.$$\displaystyle {\frac{}{}}$ - $\displaystyle \partial_{XX}^{}$B(1/2)$\displaystyle \left.\vphantom{ \frac{}{} - \partial_{XX} B^{(1/2)} }\right]$  , (C.36)


L'équation [[*]] nous donne :

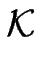B(3/2) = - $\displaystyle \cal {K}$(1)  ; (C.37)

et l'équation [[*]] :
$\displaystyle \cal {H}$(0) $\displaystyle \left[\vphantom{ A^{(3/2)} + c^{(3/2)} + \frac{b^{(3/2)}}{2} + \frac{a^{(3/2)}}{3} }\right.$A(3/2) + c(3/2) + $\displaystyle {\frac{b^{(3/2)}}{2}}$ + $\displaystyle {\frac{a^{(3/2)}}{3}}$$\displaystyle \left.\vphantom{ A^{(3/2)} + c^{(3/2)} + \frac{b^{(3/2)}}{2} + \frac{a^{(3/2)}}{3} }\right]$ = $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \left[\vphantom{ \frac{\partial_X b^{(1)}}{6} + \frac{\partial_X a^{(1)}}{2} + \partial_X A^{(1)} + \partial_X B^{(1)} }\right.$$\displaystyle {\frac{\partial_X b^{(1)}}{6}}$ + $\displaystyle {\frac{\partial_X a^{(1)}}{2}}$ + $\displaystyle \partial_{X}^{}$A(1) + $\displaystyle \partial_{X}^{}$B(1)$\displaystyle \left.\vphantom{ \frac{\partial_X b^{(1)}}{6} + \frac{\partial_X a^{(1)}}{2} + \partial_X A^{(1)} + \partial_X B^{(1)} }\right]$  
  + $\displaystyle \partial_{X}^{}$H(1/2) $\displaystyle \left[\vphantom{ \partial_X a^{(1/2)} + \partial_X A^{(1/2)} + \partial_X B^{(1/2)} }\right.$$\displaystyle \partial_{X}^{}$a(1/2) + $\displaystyle \partial_{X}^{}$A(1/2) + $\displaystyle \partial_{X}^{}$B(1/2)$\displaystyle \left.\vphantom{ \partial_X a^{(1/2)} + \partial_X A^{(1/2)} + \partial_X B^{(1/2)} }\right]$  
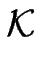  - $\displaystyle \partial_{X}^{}$H(1) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(0) - $\displaystyle \cal {H}$(1) $\displaystyle \left[\vphantom{ A^{(1/2)} - {\cal S}^{(0)} }\right.$A(1/2) - $\displaystyle \cal {S}$(0)$\displaystyle \left.\vphantom{ A^{(1/2)} - {\cal S}^{(0)} }\right]$  
  - $\displaystyle \cal {H}$(1/2) $\displaystyle \left[\vphantom{ A^{(1)} + a^{(1)} + \frac{b^{(1)}}{2} }\right.$A(1) + a(1) + $\displaystyle {\frac{b^{(1)}}{2}}$$\displaystyle \left.\vphantom{ A^{(1)} + a^{(1)} + \frac{b^{(1)}}{2} }\right]$  
  - $\displaystyle \cal {H}$(1) $\displaystyle \left[\vphantom{ A^{(1/2)} + 2 \, a^{(1/2)} }\right.$A(1/2) + 2 a(1/2)$\displaystyle \left.\vphantom{ A^{(1/2)} + 2 \, a^{(1/2)} }\right]$  . (C.38)


L'équation de conservation de la masse [[*]] apporte à cet ordre :

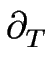$\displaystyle \partial_{T}^{}$H(1/2) = $\displaystyle \cal {H}$(0) A(3/2) + $\displaystyle \cal {H}$(1/2) A(1) + $\displaystyle \cal {H}$(1) A(1/2)  
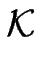  - $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{X}^{}$B(1) - $\displaystyle \partial_{X}^{}$H(1/2) $\displaystyle \partial_{X}^{}$B(1/2) + $\displaystyle \partial_{X}^{}$H(1) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(0)  
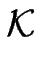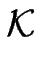  - $\displaystyle \beta$ $\displaystyle \partial_{X}^{}$$\displaystyle \left(\vphantom{ {\cal L}^{(0)} \, \partial_X {\cal K}^{(1/2)} + {\cal L}^{(1/2)} \, \partial_X {\cal K}^{(0)} }\right.$$\displaystyle \cal {L}$(0) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(1/2) + $\displaystyle \cal {L}$(1/2) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(0)$\displaystyle \left.\vphantom{ {\cal L}^{(0)} \, \partial_X {\cal K}^{(1/2)} + {\cal L}^{(1/2)} \, \partial_X {\cal K}^{(0)} }\right)$  , (C.39)


En utilisant les valeurs précédemment déterminées des diverses constantes ( A(i), B(i), a(i), ... ), on obtient la contribution sous-dominante à l'équation d'évolution du méandre :

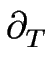$\displaystyle \partial_{T}^{}$H(1/2) = - $\displaystyle \partial_{X}^{}$$\displaystyle \left[\vphantom{ \frac{\eta}{2} \, \frac{\partial_X H^{(1/2)}}{{\... ... \, \left( \frac{1}{{\cal H}^{(0)}} -1 \right) \, \partial_X H^{(1/2)} }\right.$$\displaystyle {\frac{\eta}{2}}$ $\displaystyle {\frac{\partial_X H^{(1/2)}}{{\cal H}^{(0)}}}$ + $\displaystyle {\frac{\eta}{{\cal H}^{(0)}}}$ $\displaystyle \left(\vphantom{ \frac{1}{{\cal H}^{(0)}} -1 }\right.$$\displaystyle {\frac{1}{{\cal H}^{(0)}}}$ - 1$\displaystyle \left.\vphantom{ \frac{1}{{\cal H}^{(0)}} -1 }\right)$ $\displaystyle \partial_{X}^{}$H(1/2)  
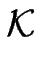    + $\displaystyle {\frac{1}{{\cal H}^{(0)}}}$ $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(1/2) - 2 $\displaystyle \left(\vphantom{ \frac{1}{{\cal H}^{(0)}} }\right.$$\displaystyle {\frac{1}{{\cal H}^{(0)}}}$$\displaystyle \left.\vphantom{ \frac{1}{{\cal H}^{(0)}} }\right)^{2}_{}$ $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{X}^{}$H(1/2) $\displaystyle \partial_{X}^{}$$\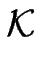displaystyle \cal {K}$(0)  
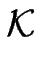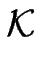    + $\displaystyle \beta$$\displaystyle \left(\vphantom{ {\cal L}^{(0)} \, \partial_X {\cal K}^{(1/2)} + {\cal L}^{(1/2)} \, \partial_X {\cal K}^{(0)} }\right.$$\displaystyle \cal {L}$(0) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(1/2) + $\displaystyle \cal {L}$(1/2) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(0)$\displaystyle \left.\vphantom{ {\cal L}^{(0)} \, \partial_X {\cal K}^{(1/2)} + {\cal L}^{(1/2)} \, \partial_X {\cal K}^{(0)} }\right)$  
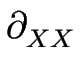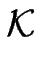    + $\displaystyle {\frac{1}{2 \, ({\cal H}^{(0)})^2}}$ $\displaystyle \partial_{XX}^{}$H(0) $\displaystyle \partial_{X}^{}$$\displaystyle \cal {K}$(0)  
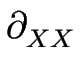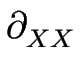    $\displaystyle \left.\vphantom{ + \frac{\eta}{3 \, ({\cal H}^{(0)})^3} \, \parti... ... \, ({\cal H}^{(0)})^2} \, \partial_X H^{(0)} \, \partial_{XX} H^{(0)} }\right.$ + $\displaystyle {\frac{\eta}{3 \, ({\cal H}^{(0)})^3}}$ $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{XX}^{}$H(0) + $\displaystyle {\frac{\eta}{6 \, ({\cal H}^{(0)})^2}}$ $\displaystyle \partial_{X}^{}$H(0) $\displaystyle \partial_{XX}^{}$H(0)$\displaystyle \left.\vphantom{ + \frac{\eta}{3 \, ({\cal H}^{(0)})^3} \, \parti... ... \, ({\cal H}^{(0)})^2} \, \partial_X H^{(0)} \, \partial_{XX} H^{(0)} }\right]$  .  
      (C.40)

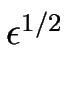En posant $ \tilde{H}$ = H(0) + $ \epsilon^{1/2}_{}$ H(1/2) ainsi que

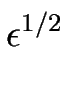$\displaystyle \tilde{\cal H}$ = $\displaystyle \cal {H}$(0) + $\displaystyle \epsilon^{1/2}_{}$ $\displaystyle \cal {H}$(1/2)  ,  
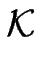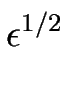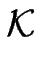$\displaystyle \tilde{\cal K}$ = $\displaystyle \cal {K}$(0) + $\displaystyle \epsilon^{1/2}_{}$ $\displaystyle \cal {K}$(1/2)  ,  
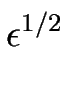$\displaystyle \tilde{\cal L}$ = $\displaystyle \cal {L}$(0) + $\displaystyle \epsilon^{1/2}_{}$ $\displaystyle \cal {L}$(1/2)  .  

et en combinant les équations [[*]] et [[*]], on obtient une équation fermée pour $ \tilde{H}$ :
$\displaystyle \partial_{T}^{}$$\displaystyle \tilde{H}$ = - $\displaystyle \partial_{X}^{}$$\displaystyle \left[\vphantom{ \frac{\eta}{2} \, \frac{\partial_X {\tilde H}}{{... ...( \frac{1}{{\tilde {\cal L}}} + 2 \, {\tilde {\cal L}} \right) \right) }\right.$$\displaystyle {\frac{\eta}{2}}$ $\displaystyle {\frac{\partial_X {\tilde H}}{{\tilde {\cal H}}}}$$\displaystyle \left(\vphantom{ 1 + \epsilon^{1/2} \, \frac{\partial_{XX} {\tild... ...}} \left( \frac{1}{{\tilde {\cal L}}} + 2 \, {\tilde {\cal L}} \right) }\right.$1 + $\displaystyle \epsilon^{1/2}_{}$ $\displaystyle {\frac{\partial_{XX} {\tilde H}}{3 \, {\tilde {\cal H}}^{3/2}}}$$\displaystyle \left(\vphantom{ \frac{1}{{\tilde {\cal L}}} + 2 \, {\tilde {\cal L}} }\right.$$\displaystyle {\frac{1}{{\tilde {\cal L}}}}$ + 2 $\displaystyle \tilde{\cal L}$$\displaystyle \left.\vphantom{ \frac{1}{{\tilde {\cal L}}} + 2 \, {\tilde {\cal L}} }\right)$$\displaystyle \left.\vphantom{ 1 + \epsilon^{1/2} \, \frac{\partial_{XX} {\tild... ...}} \left( \frac{1}{{\tilde {\cal L}}} + 2 \, {\tilde {\cal L}} \right) }\right)$  
    + $\displaystyle \left.\vphantom{ \left( \frac{1}{\tilde {\cal H}} + \beta {\tilde... ... H}}{2 \, {\tilde {\cal H}}^2} \right) \, \partial_X {\tilde {\cal K}} }\right.$$\displaystyle \left(\vphantom{ \frac{1}{\tilde {\cal H}} + \beta {\tilde {\cal ... ...lon^{1/2} \, \frac{\partial_{XX} {\tilde H}}{2 \, {\tilde {\cal H}}^2} }\right.$$\displaystyle {\frac{1}{\tilde {\cal H}}}$ + $\displaystyle \beta$$\displaystyle \tilde{\cal L}$ + $\displaystyle \epsilon^{1/2}_{}$ $\displaystyle {\frac{\partial_{XX} {\tilde H}}{2 \, {\tilde {\cal H}}^2}}$$\displaystyle \left.\vphantom{ \frac{1}{\tilde {\cal H}} + \beta {\tilde {\cal ... ...lon^{1/2} \, \frac{\partial_{XX} {\tilde H}}{2 \, {\tilde {\cal H}}^2} }\right)$ $\displaystyle \partial_{X}^{}$$\displaystyle \tilde{\cal K}$$\displaystyle \left.\vphantom{ \left( \frac{1}{\tilde {\cal H}} + \beta {\tilde... ... H}}{2 \, {\tilde {\cal H}}^2} \right) \, \partial_X {\tilde {\cal K}} }\right]$ (C.41)


En revenant aux variables physiques, on obtient l'équation suivante décrite au chapitre [*] :

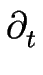$\displaystyle \partial_{t}^{}$$\displaystyle \zeta$ = - $\displaystyle \partial_{x}^{}$$\displaystyle \left[\vphantom{ \frac{\Omega F \ell^2}{2} \; \frac{\partial_x \z... ..._x \zeta)^2} + \frac{2}{\sqrt{1+(\partial_x \zeta)^2}} \right) \right) }\right.$$\displaystyle {\frac{\Omega F \ell^2}{2}}$  $\displaystyle {\frac{\partial_x \zeta}{(1+(\partial_x\zeta)^2)}}$$\displaystyle \left(\vphantom{ 1 - \frac{\kappa \, \ell}{3} \left( \sqrt{1+(\partial_x \zeta)^2} + \frac{2}{\sqrt{1+(\partial_x \zeta)^2}} \right) }\right.$1 - $\displaystyle {\frac{\kappa \, \ell}{3}}$$\displaystyle \left(\vphantom{ \sqrt{1+(\partial_x \zeta)^2} + \frac{2}{\sqrt{1+(\partial_x \zeta)^2}} }\right.$$\displaystyle \sqrt{1+(\partial_x \zeta)^2}$ + $\displaystyle {\frac{2}{\sqrt{1+(\partial_x \zeta)^2}}}$$\displaystyle \left.\vphantom{ \sqrt{1+(\partial_x \zeta)^2} + \frac{2}{\sqrt{1+(\partial_x \zeta)^2}} }\right)$$\displaystyle \left.\vphantom{ 1 - \frac{\kappa \, \ell}{3} \left( \sqrt{1+(\partial_x \zeta)^2} + \frac{2}{\sqrt{1+(\partial_x \zeta)^2}} \right) }\right)$  
    $\displaystyle \left.\vphantom{ - \left( \left( \frac{D_S \ell}{\sqrt{1+(\partia... ...right) \frac{\partial_x (\Gamma \kappa)}{\sqrt{1+(\partial_x\zeta)^2}} }\right.$ - $\displaystyle \left(\vphantom{ \left( \frac{D_S \ell}{\sqrt{1+(\partial_x \zeta)^2}} + D_L a \right) - \frac{D_S \, \ell^2 \, \kappa}{2} }\right.$$\displaystyle \left(\vphantom{ \frac{D_S \ell}{\sqrt{1+(\partial_x \zeta)^2}} + D_L a }\right.$$\displaystyle {\frac{D_S \ell}{\sqrt{1+(\partial_x \zeta)^2}}}$ + DLa$\displaystyle \left.\vphantom{ \frac{D_S \ell}{\sqrt{1+(\partial_x \zeta)^2}} + D_L a }\right)$ - $\displaystyle {\frac{D_S \, \ell^2 \, \kappa}{2}}$$\displaystyle \left.\vphantom{ \left( \frac{D_S \ell}{\sqrt{1+(\partial_x \zeta)^2}} + D_L a \right) - \frac{D_S \, \ell^2 \, \kappa}{2} }\right)$$\displaystyle {\frac{\partial_x (\Gamma \kappa)}{\sqrt{1+(\partial_x\zeta)^2}}}$$\displaystyle \left.\vphantom{ - \left( \left( \frac{D_S \ell}{\sqrt{1+(\partia... ...right) \frac{\partial_x (\Gamma \kappa)}{\sqrt{1+(\partial_x\zeta)^2}} }\right]$  ,  
      (C.42)

où $ \kappa$ est la courbure de la marche, définie par :

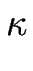$\displaystyle \kappa$ = - $\displaystyle {\frac{\partial_{xx} \zeta}{\left( 1 + \left( \partial_x \zeta \right)^2 \right)^{3/2}}}$ (C.43)

next up previous contents
suivant: Cas général : avec monter: Cas en phase précédent: Ordre dominant   Table des matières
fred 2001-07-02