


suivant: Termes sous-dominants
monter: Cas général : avec
précédent: Cas général : avec
Table des matières
Dans ce qui suit, on a pris 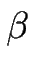 = 0 ; c'est-à-dire que l'on n'a pas pris en compte l'effet de diffusion de ligne.
À partir de l'analyse de stabilité linéaire du train de marches, on obtient la relation de dispersion linéaire suivante, développée pour de faibles déphasages
= 0 ; c'est-à-dire que l'on n'a pas pris en compte l'effet de diffusion de ligne.
À partir de l'analyse de stabilité linéaire du train de marches, on obtient la relation de dispersion linéaire suivante, développée pour de faibles déphasages 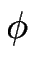 et de grandes longueurs d'onde
q
et de grandes longueurs d'onde
q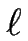
 1 :
1 :
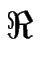 e( e(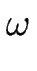  ) ) |
= |
     (q (q )2 - )2 -  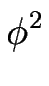  - -  (q (q )4 , )4 , |
|
| |
|
|
(C.44) |
 m( m(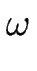  ) ) |
= |
 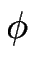 . . |
(C.45) |
Le méandre est stable vis-à-vis de faibles perturbations lorsque
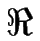 e(
e( ) < 0 et instable lorsque la partie réelle du taux de croissance
) < 0 et instable lorsque la partie réelle du taux de croissance  est positive.
est positive.
Afin d'exprimer la dynamique du train de marches proche du seuil de l'instabilité, nous avons besoin d'identifier un petit paramètre qui mesure l'écart à ce seuil.
Dans ce qui suit, nous considérerons le cas couramment rencontré expérimentalement où il existe un effet Ehrlich-Schwoebel (i.e. d- > d+).
Sous cette condition, la surface vicinale est instable vis-à-vis de l'instabilité de méandre dès que la croissance a lieu : le seuil de l'instabilité doit être proportionnel au flux de matière incident F.
Posons alors
En conditions expérimentales habituelles, ce paramètre est petit.
Le mode le plus instable (i.e. le mode dont le taux de croissance est le plus important) est obtenu pour :
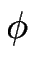 = 0 = 0
|
|
et
et son taux de croissance s'écrit :
Un examen attentif de l'équation [![[*]](crossref.gif) ] nous montre que les modes instables sont ceux pour lesquels
q
] nous montre que les modes instables sont ceux pour lesquels
q 
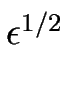 et
et
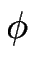

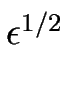 (voir figure [
(voir figure [![[*]](crossref.gif) ]).
]).
Figure:
Taux de croissance de la perturbation en fonction de q et 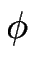 . Les modes instables sont ceux pour lesquels
. Les modes instables sont ceux pour lesquels
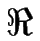 e(
e( ) > 0 et sont représentés en blanc sur la figure.
) > 0 et sont représentés en blanc sur la figure.
|
|
Cela nous donne les échelles spatiales naturelles sur lesquelles se développe le méandre. Nous avons :
m étant le nombre caractéristique de marches sur lequel la modulation de phase peut être détectée. C'est-à-dire que le déphasage entre marches adjacentes est extrêmement faible et est d'ordre 1 entre la marche n et la marche n + m.
Les échelles de temps caractéristiques de l'instabilité sont données par le taux de croissance  . La dynamique du méandre avec liberté de phase fait intervenir deux échelles de temps distinctes.
La plus rapide est celle associée à la partie imaginaire de
. La dynamique du méandre avec liberté de phase fait intervenir deux échelles de temps distinctes.
La plus rapide est celle associée à la partie imaginaire de  et est reliée aux effets propagatifs (on a
et est reliée aux effets propagatifs (on a
 m(
m( )
) 
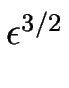 et l'échelle de temps associée
et l'échelle de temps associée


 ). L'échelle de temps lente
). L'échelle de temps lente  est celle reliée au développement de l'instabilité et est donnée par la partie réelle de
est celle reliée au développement de l'instabilité et est donnée par la partie réelle de  :
:


 .
.
Afin de décrire la dynamique non linéaire de l'instabilité, nous avons besoin de connaître le comportement d'échelle de l'amplitude du méandre pour lequel les non-linéarités deviennent pertinentes. Au chapitre ![[*]](crossref.gif) , il a été montré que
, il a été montré que


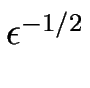 .
.
Nous pouvons maintenant effectuer un développement multi-échelle des équations constitutives du modèle.
Pour simplifier les calculs, nous travaillerons avec le champ concentration réduit
um = 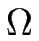 (cm - ceq). Comme cela est montré au chapitre
(cm - ceq). Comme cela est montré au chapitre ![[*]](crossref.gif) , um est proportionnel à la racine carrée de
, um est proportionnel à la racine carrée de  .
.
Afin de rendre explicite la dépendance en  , on pose :
, on pose :
x = 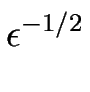 X, t = X, t =  T3/2 + T3/2 +  T2, um = T2, um =  Um, Um,  = =  Hm , Hm ,
|
(C.48) |
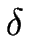 fm = fm + 1 - fm est de l'ordre du déphasage
fm = fm + 1 - fm est de l'ordre du déphasage 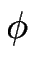 . Comme
. Comme
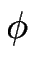

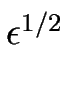 , on introduit l'opérateur de différence finie renormalisé
, on introduit l'opérateur de différence finie renormalisé  , défini par
, défini par
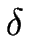 fm =
fm = 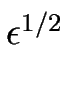
 fm.
fm.
Dans le but d'extraire les échelles en  des conditions limites, on effectue le changement de variable suivant :
des conditions limites, on effectue le changement de variable suivant :
 = (z - zm(x, t))/(zm + 1(x, t) - zm(x, t)).
Alors, la loi de conservation de la matière sur les terrasses s'écrit :
= (z - zm(x, t))/(zm + 1(x, t) - zm(x, t)).
Alors, la loi de conservation de la matière sur les terrasses s'écrit :
| 0 |
= |
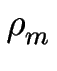  m m  Um - 2 Um - 2   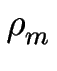  Hm Hm  Um Um |
|
| |
|
-2  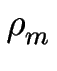  Hm Hm  Um - Um -  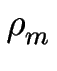 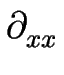 Hm Hm  Um Um |
|
| |
|
-2    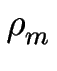  Hm Hm  Um + Um + 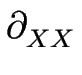 Um - 2 Um - 2   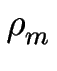   Hm Hm  Um Um |
|
| |
|
-   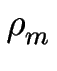 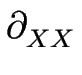  Hm Hm  Um - 2 Um - 2    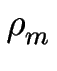   Hm Hm  Um Um |
|
| |
|
-   2 2  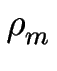   Hm Hm  Um + Um +  / / . . |
(C.49) |
Les équations cinétiques prennent la forme suivante :
 m m  Um(0) Um(0) |
- |
  Hm Hm  Um(0) = Um(0) =    Um(0) - Um(0) -  m m![$\displaystyle \left.\vphantom{ \frac{}{} U_m(0) - {\cal K}_m }\right]$](img1407.gif) , , |
(C.50) |
| |
|
|
|
 m m  Um(1) Um(1) |
- |
   Hm + Hm +    Hm Hm  Um(1) = Um(1) = |
|
| |
|
-      Um(1) - Um(1) -  m - m -    m m![$\displaystyle \left.\vphantom{ \frac{}{} U_m(1) - {\cal K}_m - \epsilon^{1/2} \Delta {\cal K}_m }\right]$](img1415.gif) . . |
(C.51) |
Et l'équation de conservation de la matière aux marches conduit à :
 |
+ |
  Hm + Hm +   Hm = Hm =   m m  Um(0) - Um(0) -   Hm Hm Um(0) Um(0)![$\displaystyle \left.\vphantom{ {\cal H}_m \; \partial_{{\cal Z}} U_m(0) - \, \epsilon^{1/2} \; \partial_X H_m \partial_X U_m(0) }\right]$](img1422.gif) |
|
| |
|
-   m m  Um(1) - Um(1) -    Hm + Hm +    Hm Hm  Um(1) Um(1)![$\displaystyle \left.\vphantom{ {\cal I}_m \; \partial_{{\cal Z}} U_m(1) - \epsi...
... H_m + \epsilon^{1/2} \partial_X \Delta H_m \right) \partial_X U_m (1) }\right]$](img1424.gif) |
|
| |
|
+     m m  Um(1) - Um(1) -    Hm + Hm +    Hm Hm  Um(1) Um(1)![$\displaystyle \left.\vphantom{ {\cal I}_m \; \partial_{{\cal Z}} U_m(1) - \epsi...
... H_m + \epsilon^{1/2} \partial_X \Delta H_m \right) \partial_X U_m (1) }\right]$](img1424.gif) |
|
| |
|
-     m m  Um(1) - Um(1) -    Hm + Hm +    Hm Hm  Um(1) Um(1)![$\displaystyle \left.\vphantom{ {\cal I}_m \; \partial_{{\cal Z}} U_m(1) - \epsi...
... H_m + \epsilon^{1/2} \partial_X \Delta H_m \right) \partial_X U_m (1) }\right]$](img1424.gif) |
|
| |
|
+ ... |
(C.52) |
où, pour simplifier, nous avons posé :
 Hm Hm |
= |
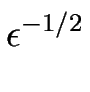 (Hm + 1 - Hm) = (Hm + 1 - Hm) =  - -  |
(C.53) |
 |
= |
zm + 1 - zm =  + +  Hm Hm |
(C.54) |
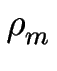 |
= |
 |
(C.55) |
 m m |
= |
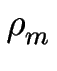 (1 + ( (1 + ( Hm)2) Hm)2) |
(C.56) |
 m m |
= |
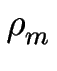 (1 + ( (1 + ( Hm + 1)2) Hm + 1)2) |
|
| |
= |
 m + 2 m + 2 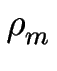  Hm Hm  Hm + Hm +  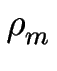 ( (  Hm)2 Hm)2 |
(C.57) |
 m m |
= |
(1 + ( Hm)2)1/2 Hm)2)1/2 |
(C.58) |
 m m |
= |
-  ceq0 ceq0 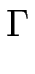  . . |
(C.59) |
En faisant l'hypothèse que Um et Hm sont des fonctions analytiques de
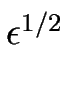 nous pouvons résoudre les équations précédentes en utilisant un développement multi-échelle.
Pour ceci on pose :
nous pouvons résoudre les équations précédentes en utilisant un développement multi-échelle.
Pour ceci on pose :
| Um |
= |
Um(0) +  Um(1/2) + Um(1/2) +  Um(1) + ... Um(1) + ... |
(C.60) |
| Hm |
= |
Hm(0) +  Hm(1/2) + Hm(1/2) +  Hm(1) + ... Hm(1) + ... |
(C.61) |
Les équations du modèle se résolvent alors en ordre successif en  .
.
Ordre 0
À cet ordre, l'équation [![[*]](crossref.gif) ] s'écrit :
] s'écrit :
 Um(0) = 0 , Um(0) = 0 ,
|
(C.62) |
ce qui implique
Um(0) = am(0) + bm(0). Les équations [
+ bm(0). Les équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] nous fournissent deux équations linéaires pour am(0) et bm(0).
Leur résolution conduit à :
] nous fournissent deux équations linéaires pour am(0) et bm(0).
Leur résolution conduit à :
| am(0) |
= |
0 |
(C.63) |
| bm(0) |
= |
 m(0) . m(0) . |
(C.64) |
À cet ordre, l'équation [![[*]](crossref.gif) ] n'apporte aucune contribution à la vitesse des marches.
] n'apporte aucune contribution à la vitesse des marches.
Ordre 1/2
À partir de l'équation [![[*]](crossref.gif) ], la composante d'ordre 1/2 de Um obéit à l'équation inhomogène suivante :
], la composante d'ordre 1/2 de Um obéit à l'équation inhomogène suivante :
dont la solution générale s'écrit :
Um(1/2)( ) = ) =   2 + am(1/2) 2 + am(1/2) + bm(1/2) + bm(1/2)
|
(C.66) |
avec
cm(1/2) = - 1/(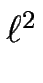

 m(0)).
À partir des conditions limites [
m(0)).
À partir des conditions limites [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ], on obtient :
], on obtient :
 m(0) m(0) Um(1/2)(0) - Um(1/2)(0) -  Hm(0) Hm(0) Um(0)(0) Um(0)(0) |
= |
  Um(1/2)(0) - Um(1/2)(0) -  m(0) m(0)![$\displaystyle \left.\vphantom{ U_m^{(1/2)}(0) - {\cal K}_m^{(0)} }\right]$](img1433.gif) |
|
| |
|
|
(C.67) |
 m(0) m(0) Um(1/2)(1) - Um(1/2)(1) -  Hm(0) Hm(0) Um(0)(1) Um(0)(1) |
= |
-   Um(1/2)(1) Um(1/2)(1)  m(1/2) - m(1/2) -   m(0) m(0)![$\displaystyle \left.\vphantom{ U_m^{(1/2)}(1) \ {\cal K}_m^{(1/2)} - \Delta {\cal K}_m^{(0)} }\right]$](img1436.gif) . . |
|
| |
|
|
(C.68) |
Où Um(0) a été remplacé par sa valeur
 m(0) afin de rendre l'écriture plus légère.
Ces deux équations nous fournissent un système linéaire dont
am(1/2) et
bm(1/2) sont solutions.
m(0) afin de rendre l'écriture plus légère.
Ces deux équations nous fournissent un système linéaire dont
am(1/2) et
bm(1/2) sont solutions.
L'équation [![[*]](crossref.gif) ] nous donne à cet ordre sa première contribution :
] nous donne à cet ordre sa première contribution :
 + +   Hm(0) Hm(0) |
= |
  m(0) m(0) Um(1/2)( Um(1/2)( = 0) - = 0) -  Hm(0) Hm(0) Um(0) Um(0)![$\displaystyle \left.\vphantom{ {\cal H}_m^{(0)} \partial_{\cal Z} U_m^{(1/2)} ({\cal Z}=0) - \partial_X H_m^{(0)} \partial_X U_m^{(0)} }\right]$](img1440.gif) |
|
| |
- |
  m(0) m(0) Um(1/2)( Um(1/2)( = 1) - = 1) -  Hm(0) Hm(0) Um(0) Um(0)![$\displaystyle \left.\vphantom{ {\cal H}_m^{(0)} \partial_{\cal Z} U_m^{(1/2)}({\cal Z}=1) - \partial_X H_m^{(0)} \partial_X U_m^{(0)} }\right]$](img1442.gif) |
(C.69) |
| |
|
|
|
| |
= |
-  m(0)cm(1/2) m(0)cm(1/2) |
(C.70) |
| |
|
|
|
| |
= |
 + +  . . |
(C.71) |
Soit :
On reconnaît dans ce terme la première contribution de effets propagatifs.
Ordre 1
À cet ordre, l'équation [![[*]](crossref.gif) ] nous donnera l'équation dynamique désirée pour le méandre. D'après l'équation [
] nous donnera l'équation dynamique désirée pour le méandre. D'après l'équation [![[*]](crossref.gif) ], Um(1) obéit à :
], Um(1) obéit à :
 Um(1) Um(1) |
= |
   2 2   Hm(0) Hm(0) Um(1/2) + 2 Um(1/2) + 2  Hm(0) Hm(0) Um(1/2) Um(1/2) |
|
| |
|
+  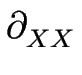 Hm(0) Hm(0) Um(1/2) + 2 Um(1/2) + 2   Hm(0) Hm(0)  Um(0) Um(0) |
|
| |
|
-   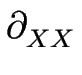 Um(0) - Um(0) -    m(0) + m(0) +   m(1/2) m(1/2)  Um(1/2) Um(1/2)![$\displaystyle \left.\vphantom{ \frac{}{} \partial_{XX} U_m^{(0)} - \left( \rho_...
...o_m^{(0)} {\cal H}_m^{(1/2)} \right) \, \partial_{\cal ZZ} U_m^{(1/2)} }\right]$](img1451.gif) |
(C.73) |
| |
= |
   2 2   Hm(0)cm(1/2) + 2 Hm(0)cm(1/2) + 2  Hm(0) Hm(0) cm(1/2) + cm(1/2) +  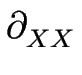 cm(1/2) cm(1/2)![$\displaystyle \left.\vphantom{ \frac{}{} 2 \partial_X \rho_m^{(0)} \partial_X H...
...^{(0)} \partial_X c_m^{(1/2)} + \rho_m^{(0)} \partial_{XX} c_m^{(1/2)} }\right]$](img1454.gif) |
|
| |
+ |
   2 2   Hm(0)am(1/2) + 2 Hm(0)am(1/2) + 2  Hm(0) Hm(0) am(1/2) am(1/2) |
|
| |
|
+    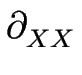 Hm(0)am(1/2) - Hm(0)am(1/2) - 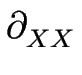  m(0) - m(0) -    m(0) + m(0) +   m(1/2) m(1/2) cm(1/2) cm(1/2)![$\displaystyle \left.\vphantom{ \frac{}{} \rho_m^{(0)} \partial_{XX} H_m^{(0)} a...
...al H}_m^{(0)} + \rho_m^{(0)} {\cal H}_m^{(1/2)} \right) \, c_m^{(1/2)} }\right]$](img1457.gif) |
|
| |
|
|
(C.74) |
| |
|
|
|
| |
= |
Am(1) + Bm(1) , + Bm(1) , |
(C.75) |
et s'écrit :
Um(1)( ) = ) =   3 + 3 +   2 + am(1) 2 + am(1) + bm(1) + bm(1)
|
(C.76) |
Les deux constantes am(1) et bm(1) sont obtenues en résolvant les équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]. La résolution de l'équation [
]. La résolution de l'équation [![[*]](crossref.gif) ] à cet ordre nous donne l'équation dynamique tant attendue :
] à cet ordre nous donne l'équation dynamique tant attendue :
   Hm(1/2) + Hm(1/2) +  Hm(0) Hm(0)![$\displaystyle \left.\vphantom{ \partial_{T_{3/2}} H_m^{(1/2)} + \partial_{T_2} H_m^{(0)} }\right]$](img1461.gif) |
= |
   m(0) m(0) Um(1)(0) + Um(1)(0) +  m(1/2) m(1/2) Um(1/2)(0) Um(1/2)(0) |
|
| |
|
  - -  Hm(0) Hm(0) Um(1/2)(0) - Um(1/2)(0) -  Hm(1/2) Hm(1/2) Um(0) Um(0)![$\displaystyle \left.\vphantom{ \frac{}{} - \partial_X H_m^{(0)} \partial_X U_m^{(1/2)} (0) - \partial_X H_m^{(1/2)} \partial_X U_m^{(0)} }\right]$](img1464.gif) |
|
| |
- |
   m(0) m(0) Um(1)(1) + Um(1)(1) +  m(1/2) m(1/2) Um(1/2)(1) Um(1/2)(1) |
|
| |
|
-  Hm(0) Hm(0) Um(1/2)(1) - Um(1/2)(1) -  Hm(1/2) Hm(1/2) Um(0)(1) Um(0)(1) |
|
| |
|
-     Hm(0) Hm(0) Um(0)(1) Um(0)(1)![$\displaystyle \left.\vphantom{ \frac{}{} \partial_X \Delta H_m^{(0)} \partial_X U_m^{(0)} (1) }\right]$](img1467.gif) |
|
| |
+ |
    m(0) m(0) Um(1/2)(1) - Um(1/2)(1) -  Hm(0) Hm(0) Um(0)(1) Um(0)(1)![$\displaystyle \left.\vphantom{ \frac{}{} {\cal H}_m^{(0)} \partial_{\cal Z} U_m^{(1/2)} (1)
- \partial_X H_m^{(0)} \partial_X U_m^{(0)} (1) }\right]$](img1469.gif) |
(C.77) |
| |
|
|
|
| |
= |
-  m(0) m(0)  + Bm(1) + Bm(1) |
|
| |
|
-2  Hm(0) Hm(0)  Hm(0) Hm(0) cm(1/2) + am(1/2) cm(1/2) + am(1/2) - -  m(1/2)cm(1/2) m(1/2)cm(1/2) |
|
| |
|
+  Hm(0) Hm(0)   + am(1/2) + am(1/2) + +   Hm(0) Hm(0)  m(0) m(0) |
|
| |
|
+    m(0) m(0) cm(1/2) + am(1/2) cm(1/2) + am(1/2) - -  Hm(0) Hm(0)  m(0) m(0)![$\displaystyle \left.\vphantom{ {\cal H}_m^{(0)} \left( c_m^{(1/2)} + a_m^{(1/2)} \right) - \partial_X H_m^{(0)} \partial_X {\cal K}_m^{(0)} }\right]$](img1478.gif) . . |
|
| |
|
|
(C.78) |
En utilisant maintenant l'expression de Am(1), Bm(1) et
cm(1/2) ainsi que la constante
am(1/2) précédemment calculée, on obtient finalement l'équation d'évolution suivante :
 Hm(1/2) Hm(1/2) |
+ |
 Hm(0) = Hm(0) =   Hm(1/2) Hm(1/2) |
|
| |
|
+ D       m(0) - m(0) -  |
|
| |
|
   (d+ + d-) (d+ + d-)  Hm(0) Hm(0)  m(0) + m(0) +  m(0) m(0)  m(0) + m(0) + 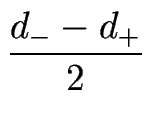   ![$\displaystyle \left.\vphantom{ \left( \frac{}{} (d_++d_-) \, \partial_X H_m^{(0...
..._m^{(0)} + \frac{d_--d_+}{2} \, \frac{\ell_m^{(0)}}{\ell^2} \right) \; }\right]$](img1486.gif) |
|
| |
|
-     Hm(0) Hm(0)  m(0) - m(0) -  |
|
| |
|
   (d+ + d-) (d+ + d-)  Hm(0) Hm(0)  m(0) + m(0) +  m(0) m(0)  m(0) - (2d+ m(0) - (2d+ m(0) + m(0) +  m(0)) m(0))  ![$\displaystyle \left.\vphantom{ \frac{}{} \left( (d_++d_-) \, \partial_X H_m^{(0...
...cal S}_m^{(0)}) \frac{\ell_m^{(0)}}{2 \ell^2 {\cal H}_m^{(0)}} \right) }\right]$](img1493.gif) |
|
| |
|
|
(C.79) |
Nous avons maintenant deux équations ([![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]) qui expriment la dynamique séparément sur les deux échelles de temps mentionnées plus haut : la rapide et la lente.
En posant
]) qui expriment la dynamique séparément sur les deux échelles de temps mentionnées plus haut : la rapide et la lente.
En posant
 = Hm(0) +
= Hm(0) + 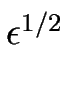 Hm(1/2) et
Hm(1/2) et
 =
= 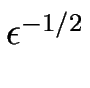 T3/2 + T2, on peut les regrouper en une seule équation :
T3/2 + T2, on peut les regrouper en une seule équation :
  = = 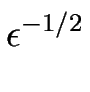  Hm(0) + Hm(0) +  Hm(1/2) + Hm(1/2) +  Hm(0) + O( Hm(0) + O( ) . ) .
|
(C.80) |
En revenant aux variables physiques, on obtient finalement :
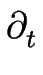  = - = -  Jm + Jm +  Gm + Gm +  F F    - -  ![$\displaystyle \left.\vphantom{ \zeta_m - \frac{\ell_m}{2} }\right]$](img1498.gif) , ,
|
(C.81) |
avec
| Jm |
= |
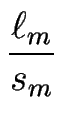  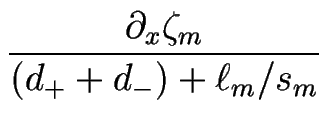   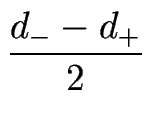  F F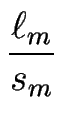 + D + D   - - 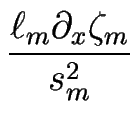    ![$\displaystyle \left.\vphantom{ \frac{d_--d_+}{2} \Omega F \frac{\ell_m}{s_m} + ...
...c{\ell_m \partial_x \zeta_m}{s_m^2} \partial_x {\bar \kappa}_m \right) }\right]$](img1503.gif) |
|
| |
|
-  D D   , , |
(C.82) |
| Gm |
= |
 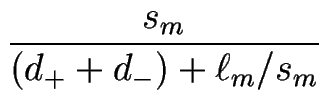   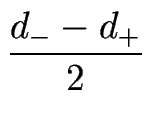  F F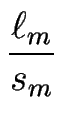 + D + D   - - 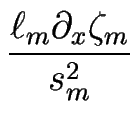    ![$\displaystyle \left.\vphantom{ \frac{d_--d_+}{2} \Omega F \frac{\ell_m}{s_m} + ...
...c{\ell_m \partial_x \zeta_m}{s_m^2} \partial_x {\bar \kappa}_m \right) }\right]$](img1503.gif) ; ; |
|
| |
|
|
(C.83) |
avec
 =
= 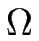 ceq0
ceq0 
 , où
, où  est la courbure du méandre
est la courbure du méandre 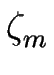 , et
sm = (1 + (
, et
sm = (1 + (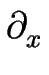
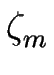 )2)1/2.
)2)1/2.
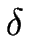 est l'opérateur de différence finie, défini pour une fonction f de la variable m par
est l'opérateur de différence finie, défini pour une fonction f de la variable m par
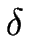 fm = fm + 1 - fm.
fm = fm + 1 - fm.
Nous avons obtenu l'équation dynamique pour la marche m.
Cette équation est couplée avec celle de la marche m + 1.
Toutes les marches de la surface sont donc couplées entre elles.
Comme le déphasage entre marche est faible proche du seuil de l'instabilité, pour étudier la dynamique de la surface vicinale, on doit prendre en compte un nombre n considérable de marches ; où
n  1/
1/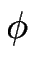 . On a alors à résoudre un système de n équations non linéaires couplées.
Cette approche, bien que plus simple que la résolution directe des équations discrètes du modèle BCF, demeure prohibitive numériquement si l'on veut étudier la dynamique à grande échelle de la surface vicinale. Le développement analytique de l'équation d'évolution de la surface peut cependant être poursuivi jusqu'à aboutir à une équation dynamique continue de la surface.
. On a alors à résoudre un système de n équations non linéaires couplées.
Cette approche, bien que plus simple que la résolution directe des équations discrètes du modèle BCF, demeure prohibitive numériquement si l'on veut étudier la dynamique à grande échelle de la surface vicinale. Le développement analytique de l'équation d'évolution de la surface peut cependant être poursuivi jusqu'à aboutir à une équation dynamique continue de la surface.
Considérons maintenant que la surface peut être représentée dans le repère fixe du laboratoire par une équation de la forme :
|
f (x, y, z, t) = 0 .
|
(C.84) |
Alors, la représentation de la surface au moyen des marches (appelons la « représentation discrète » ) s'écrit :
f (x, y, z, t) = 0 = z - 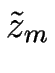 (x, t) , (x, t) ,
|
(C.85) |
avec
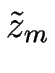 = V0t + m
= V0t + m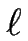 +
+ 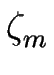 (x, t) ; y = - ma (où a est une longueur atomique) étant la hauteur de la surface au niveau de la marche m.
(x, t) ; y = - ma (où a est une longueur atomique) étant la hauteur de la surface au niveau de la marche m.
Nous pouvons aussi choisir une représentation continue de la surface au moyen d'une fonction h de x et z qui représente la hauteur de la surface en (x, z).
Nous avons alors :
|
f (x, y, z, t) = 0 = y - h(x, z, t) .
|
(C.86) |
À
z = 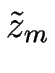 (x, t) et y = - ma, nous avons la correspondance suivante entre les deux représentations :
(x, t) et y = - ma, nous avons la correspondance suivante entre les deux représentations :
h(x, V0t + m + +  (x, t), t) = - ma . (x, t), t) = - ma .
|
(C.87) |
En utilisant cette « équation maîtresse » , nous serons capable de traduire l'ensemble des équations dynamiques de la représentation discrète en une équation d'évolution continue.
Le vecteur normal à la surface est défini par (dans le repère (x, y, z)) :
Le vecteur  , normal aux marches dans le plan (x, z) est alors donné par C.1 :
On définit aussi le vecteur
, normal aux marches dans le plan (x, z) est alors donné par C.1 :
On définit aussi le vecteur 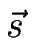 , tangent aux marches dans le plan (x, z) :
, tangent aux marches dans le plan (x, z) :
 En dérivant l'équation [
En dérivant l'équation [![[*]](crossref.gif) ] envers t et x, on obtient :
] envers t et x, on obtient :
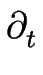 h h |
= |
- (V0 + 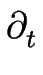  ) ) h h |
(C.91) |
  |
= |
-  . . |
(C.92) |
 Pour une fonction f définie sur la surface h, posons
fm = f (x,
Pour une fonction f définie sur la surface h, posons
fm = f (x,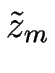 , t) ; c'est l'évaluation de la fonction f le long de la marche m. Alors :
, t) ; c'est l'évaluation de la fonction f le long de la marche m. Alors :
 |
= |
 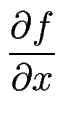  = =  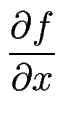  + +     |
|
| |
= |
 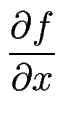  - -     |
|
| |
= |
    h h  f - f -  h h  f f |
|
| |
= |
    | h| | h|   . .   f f  . . |
|
En utilisant le fait que
 (|
(| |
| 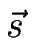 ) = 0, on a :
) = 0, on a :
 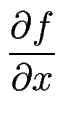  |
= |
-   . . f f |
(C.93) |
| |
= |
-    | |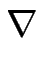 h| f h| f  . . |
(C.94) |
En appliquant l'équation [![[*]](crossref.gif) ] à
] à
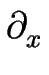
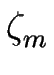 = -
= -  , on a :
, on a :
soit :
Et pour la courbure  , nous obtenons (en tenant compte de ce que la surface est vicinale :
, nous obtenons (en tenant compte de ce que la surface est vicinale :
 h = - |
h = - | h|) :
h|) :
 Il est maintenant temps d'introduire « l'approximation continue » . Comme y = - ma au niveau de la marche m, on peut considérer l'indice des marches m comme une variable continue (i.e. on s'intéressera à la hauteur h à la place de l'indice m).
Il est maintenant temps d'introduire « l'approximation continue » . Comme y = - ma au niveau de la marche m, on peut considérer l'indice des marches m comme une variable continue (i.e. on s'intéressera à la hauteur h à la place de l'indice m).
Comme le comportement d'échelle du déphasage 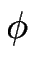 , associé à l'indice des marches m est
, associé à l'indice des marches m est
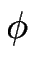

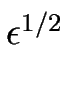 , nous avons le comportement d'échelle suivant pour la hauteur de la surface :
h
, nous avons le comportement d'échelle suivant pour la hauteur de la surface :
h 
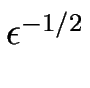 .
Le déphasage entre marches étant faible, la dynamique sera observée sur de grandes échelles de longueur ; alors
.
Le déphasage entre marches étant faible, la dynamique sera observée sur de grandes échelles de longueur ; alors


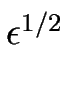 . Nous avons alors :
. Nous avons alors :
 |
= |
 + +  - -  |
|
| |
= |
 + +  + +   + O( + O( ) . ) . |
(C.97) |
Et, en dérivant l'équation [![[*]](crossref.gif) ] envers m, nous obtenons :
] envers m, nous obtenons :
Ainsi,  se récrit :
Le premier terme du membre de droite étant, compte tenu des comportements d'échelle respectifs de h et z, d'ordre un et le second d'ordre
se récrit :
Le premier terme du membre de droite étant, compte tenu des comportements d'échelle respectifs de h et z, d'ordre un et le second d'ordre
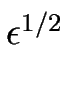 .
Comme le terme advectif de l'équation dynamique agit sur l'échelle de temps rapide, on doit pour celui-ci prendre en compte dans le développement les termes d'ordre
.
Comme le terme advectif de l'équation dynamique agit sur l'échelle de temps rapide, on doit pour celui-ci prendre en compte dans le développement les termes d'ordre
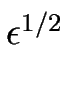 alors qu'un développement à l'ordre le plus bas est suffisant pour les autres termes pour obtenir les contributions dominantes de la dynamique.
alors qu'un développement à l'ordre le plus bas est suffisant pour les autres termes pour obtenir les contributions dominantes de la dynamique.
 Pour une fonction g dépendant de la variable m et définie sur la surface, on a
Pour une fonction g dépendant de la variable m et définie sur la surface, on a
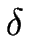 gm =
gm =  g
g -
-  g
g avec
avec
 g
g = g(x, z = zm, t). Alors :
= g(x, z = zm, t). Alors :
 gm gm |
= |
 g g - -  g g = =  + +   + O( + O( ) ) |
|
| |
= |
  + +    g + O( g + O( ) . ) . |
|
Or, d'après l'éq. [![[*]](crossref.gif) ],
],

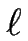 +
+ 
 =
=  + O(
+ O(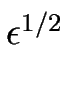 ).
Et en explicitant
).
Et en explicitant  , d'après l'éq. [
, d'après l'éq. [![[*]](crossref.gif) ], on a simplement :
], on a simplement :
On peut aussi récrire la dérivée le long de z comme une divergence :
Et, en prenant en compte le fait que
nous avons
soit :
 gm = - gm = -     g g  - -  g g  ![$\displaystyle \left.\vphantom{ \frac{\partial_x h}{\Vert \nabla h \Vert} \, g \, \vec{s} - \frac{\partial_z h}{\Vert \nabla \Vert} \, g \, \vec{n} }\right]$](img1583.gif) + O( + O( ) . ) .
|
(C.100) |
En utilisant l'équation [![[*]](crossref.gif) ], on obtient :
], on obtient :
sm =  = - = -  ; ;
|
(C.101) |
alors
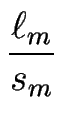 |
= |
 + O( + O( ) , ) , |
(C.102) |
 |
= |
 . . |
(C.103) |
À l'aide des équations [![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ], on a :
], on a :
soit, simplement :
En utilisant les équations [![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,
![[*]](crossref.gif) ], on peut exprimer Jm et Gm :
], on peut exprimer Jm et Gm :
| Jm |
= |
     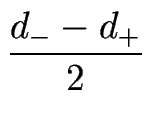  F F  + D + D   . .   ![$\displaystyle \left.\vphantom{ \frac{d_--d_+}{2} \Omega F \, \frac{a}{\Vert \na...
...a}{\Vert \nabla h \Vert} \, \vec{n} \cdot \vec{\nabla} {\bar {\cal K}} }\right]$](img1598.gif) |
|
| |
|
+  D D  . .   , , |
(C.105) |
| Gm |
= |
-      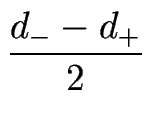  F F  + D + D   . .   ![$\displaystyle \left.\vphantom{ \frac{d_--d_+}{2} \Omega F \, \frac{a}{\Vert \na...
...a}{\Vert \nabla h \Vert} \, \vec{n} \cdot \vec{\nabla} {\bar {\cal K}} }\right]$](img1598.gif) , , |
|
| |
|
|
(C.106) |
où
 =
= 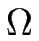 ceq0
ceq0 
 .
.
Enfin, l'équation [![[*]](crossref.gif) ], combinée avec l'équation [
], combinée avec l'équation [![[*]](crossref.gif) ], nous donne, après quelques manipulations algébriques, l'équation dynamique désirée :
], nous donne, après quelques manipulations algébriques, l'équation dynamique désirée :
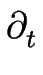 h h |
= |
- ![$\displaystyle \left(\vphantom{ \Omega F \ell - \partial_x J_m + \delta G_m + \Omega F \, \delta \left[ \zeta_m - \frac{\ell_m}{2} \right] }\right.$](img1603.gif)  F F - -  Jm + Jm +  Gm + Gm +  F F    - -  ![$\displaystyle \left.\vphantom{ \zeta_m - \frac{\ell_m}{2} }\right]$](img1498.gif) ![$\displaystyle \left.\vphantom{ \Omega F \ell - \partial_x J_m + \delta G_m + \Omega F \, \delta \left[ \zeta_m - \frac{\ell_m}{2} \right] }\right)$](img1604.gif)  h h |
|
| |
= |
-  h h ![$\displaystyle \left(\vphantom{ \Omega F \left[ \ell_m - \delta\, \frac{\ell_m}{2} \right] - \partial_x J_m + \delta G_m }\right.$](img1605.gif)  F F  - -   ![$\displaystyle \left.\vphantom{ \ell_m - \delta\, \frac{\ell_m}{2} }\right]$](img1607.gif) - -  Jm + Jm +  Gm Gm![$\displaystyle \left.\vphantom{ \Omega F \left[ \ell_m - \delta\, \frac{\ell_m}{2} \right] - \partial_x J_m + \delta G_m }\right)$](img1608.gif) . . |
(C.107) |
Les équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] permettent d'évaluer :
] permettent d'évaluer :
 Jm Jm |
= |
-     | |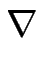 h| Jm h| Jm  ![$\displaystyle \left.\vphantom{ \frac{}{} \Vert \nabla h \Vert \, J_m \, \vec{s} }\right]$](img1610.gif) , , |
(C.108) |
 Gm Gm |
= |
-       - -    Gm Gm![$\displaystyle \left.\vphantom{ \left( \frac{\partial_z h}{\Vert \nabla h \Vert}...
... - \frac{\partial_z h}{\Vert \nabla h \Vert} \, \vec{n} \right) \, G_m }\right]$](img1615.gif) . . |
(C.109) |
Les termes propagatifs
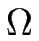 F
F et
et
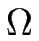 F
F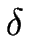
 /2 sont d'ordre supérieur ; ils doivent être évalués jusqu'à l'ordre
/2 sont d'ordre supérieur ; ils doivent être évalués jusqu'à l'ordre
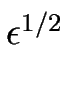 .
.
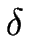
 est calculé grâce à [
est calculé grâce à [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] :
] :
En combinant tout ceci, nous obtenons finalement l'équation dynamique pour la surface dans une représentation continue :
où
 = h/a -
= h/a - 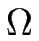 F t, c'est la hauteur de la surface, exprimée en unité atomique, à laquelle la croissance moyenne a été retranchée.
F t, c'est la hauteur de la surface, exprimée en unité atomique, à laquelle la croissance moyenne a été retranchée.
Dans la limite unilatérale (
d+ = 0, d-  +
+  ), elle prend la forme :
), elle prend la forme :



suivant: Termes sous-dominants
monter: Cas général : avec
précédent: Cas général : avec
Table des matières
fred
2001-07-02
![]() = 0 ; c'est-à-dire que l'on n'a pas pris en compte l'effet de diffusion de ligne.
À partir de l'analyse de stabilité linéaire du train de marches, on obtient la relation de dispersion linéaire suivante, développée pour de faibles déphasages
= 0 ; c'est-à-dire que l'on n'a pas pris en compte l'effet de diffusion de ligne.
À partir de l'analyse de stabilité linéaire du train de marches, on obtient la relation de dispersion linéaire suivante, développée pour de faibles déphasages ![]() et de grandes longueurs d'onde
q
et de grandes longueurs d'onde
q![]()
![]() 1 :
1 :




![[*]](crossref.gif) ] nous montre que les modes instables sont ceux pour lesquels
q
] nous montre que les modes instables sont ceux pour lesquels
q ![]()
![]() et
et
![]()
![]()
![]() (voir figure [
(voir figure [![[*]](crossref.gif) ]).
]).
![\includegraphics[height=8cm,angle=0]{../Images/im_wr.eps}](img230.gif)
![[*]](crossref.gif) , il a été montré que
, il a été montré que
![]()
![]()
![]() .
.
![]() (cm - ceq). Comme cela est montré au chapitre
(cm - ceq). Comme cela est montré au chapitre ![[*]](crossref.gif) , um est proportionnel à la racine carrée de
, um est proportionnel à la racine carrée de ![]() .
.
![]() , on pose :
, on pose :
![]() des conditions limites, on effectue le changement de variable suivant :
des conditions limites, on effectue le changement de variable suivant :
![]() = (z - zm(x, t))/(zm + 1(x, t) - zm(x, t)).
Alors, la loi de conservation de la matière sur les terrasses s'écrit :
= (z - zm(x, t))/(zm + 1(x, t) - zm(x, t)).
Alors, la loi de conservation de la matière sur les terrasses s'écrit :
 .
.![]() nous pouvons résoudre les équations précédentes en utilisant un développement multi-échelle.
Pour ceci on pose :
nous pouvons résoudre les équations précédentes en utilisant un développement multi-échelle.
Pour ceci on pose :
![[*]](crossref.gif) ] s'écrit :
] s'écrit :
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] nous fournissent deux équations linéaires pour am(0) et bm(0).
Leur résolution conduit à :
] nous fournissent deux équations linéaires pour am(0) et bm(0).
Leur résolution conduit à :
![[*]](crossref.gif) ] n'apporte aucune contribution à la vitesse des marches.
] n'apporte aucune contribution à la vitesse des marches.
![[*]](crossref.gif) ], la composante d'ordre 1/2 de Um obéit à l'équation inhomogène suivante :
], la composante d'ordre 1/2 de Um obéit à l'équation inhomogène suivante :

![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ], on obtient :
], on obtient :
![[*]](crossref.gif) ] nous donne à cet ordre sa première contribution :
] nous donne à cet ordre sa première contribution :
 .
.![[*]](crossref.gif) ] nous donnera l'équation dynamique désirée pour le méandre. D'après l'équation [
] nous donnera l'équation dynamique désirée pour le méandre. D'après l'équation [![[*]](crossref.gif) ], Um(1) obéit à :
], Um(1) obéit à :



![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]. La résolution de l'équation [
]. La résolution de l'équation [![[*]](crossref.gif) ] à cet ordre nous donne l'équation dynamique tant attendue :
] à cet ordre nous donne l'équation dynamique tant attendue :
 + am(1/2)
+ am(1/2)
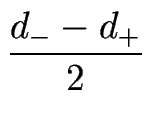


![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]) qui expriment la dynamique séparément sur les deux échelles de temps mentionnées plus haut : la rapide et la lente.
En posant
]) qui expriment la dynamique séparément sur les deux échelles de temps mentionnées plus haut : la rapide et la lente.
En posant
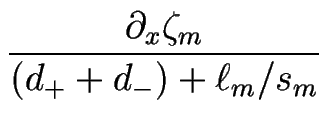
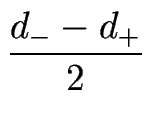
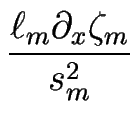
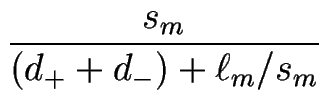
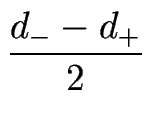
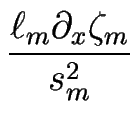
![]() 1/
1/![]() . On a alors à résoudre un système de n équations non linéaires couplées.
Cette approche, bien que plus simple que la résolution directe des équations discrètes du modèle BCF, demeure prohibitive numériquement si l'on veut étudier la dynamique à grande échelle de la surface vicinale. Le développement analytique de l'équation d'évolution de la surface peut cependant être poursuivi jusqu'à aboutir à une équation dynamique continue de la surface.
. On a alors à résoudre un système de n équations non linéaires couplées.
Cette approche, bien que plus simple que la résolution directe des équations discrètes du modèle BCF, demeure prohibitive numériquement si l'on veut étudier la dynamique à grande échelle de la surface vicinale. Le développement analytique de l'équation d'évolution de la surface peut cependant être poursuivi jusqu'à aboutir à une équation dynamique continue de la surface.
![]() (x, t) et y = - ma, nous avons la correspondance suivante entre les deux représentations :
(x, t) et y = - ma, nous avons la correspondance suivante entre les deux représentations :
 =
= 





![]() En dérivant l'équation [
En dérivant l'équation [![[*]](crossref.gif) ] envers t et x, on obtient :
] envers t et x, on obtient :
![]() Pour une fonction f définie sur la surface h, posons
fm = f (x,
Pour une fonction f définie sur la surface h, posons
fm = f (x,![]() , t) ; c'est l'évaluation de la fonction f le long de la marche m. Alors :
, t) ; c'est l'évaluation de la fonction f le long de la marche m. Alors :
![[*]](crossref.gif) ] à
] à
![]()
![]() = -
= - ![]() , on a :
, on a :

 .
. = -
= -  =
= ![]() Il est maintenant temps d'introduire « l'approximation continue » . Comme y = - ma au niveau de la marche m, on peut considérer l'indice des marches m comme une variable continue (i.e. on s'intéressera à la hauteur h à la place de l'indice m).
Il est maintenant temps d'introduire « l'approximation continue » . Comme y = - ma au niveau de la marche m, on peut considérer l'indice des marches m comme une variable continue (i.e. on s'intéressera à la hauteur h à la place de l'indice m).
![]() , associé à l'indice des marches m est
, associé à l'indice des marches m est
![]()
![]()
![]() , nous avons le comportement d'échelle suivant pour la hauteur de la surface :
h
, nous avons le comportement d'échelle suivant pour la hauteur de la surface :
h ![]()
![]() .
Le déphasage entre marches étant faible, la dynamique sera observée sur de grandes échelles de longueur ; alors
.
Le déphasage entre marches étant faible, la dynamique sera observée sur de grandes échelles de longueur ; alors
![]()
![]()
![]() . Nous avons alors :
. Nous avons alors :
![[*]](crossref.gif) ] envers m, nous obtenons :
] envers m, nous obtenons :

![]() Pour une fonction g dépendant de la variable m et définie sur la surface, on a
Pour une fonction g dépendant de la variable m et définie sur la surface, on a
![]() gm =
gm = ![]() g
g![]() -
- ![]() g
g![]() avec
avec
![]() g
g![]() = g(x, z = zm, t). Alors :
= g(x, z = zm, t). Alors :
![[*]](crossref.gif) ],
],
![[*]](crossref.gif) ], on a simplement :
], on a simplement :

 g
g ![[*]](crossref.gif) ], on obtient :
], on obtient :
![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ], on a :
], on a :
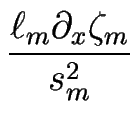


![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,![[*]](crossref.gif) ,
,
![[*]](crossref.gif) ], on peut exprimer Jm et Gm :
], on peut exprimer Jm et Gm :


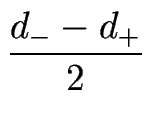
 + D
+ D 
 D
D 

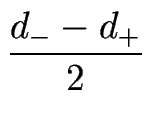
 + D
+ D 
![[*]](crossref.gif) ], combinée avec l'équation [
], combinée avec l'équation [![[*]](crossref.gif) ], nous donne, après quelques manipulations algébriques, l'équation dynamique désirée :
], nous donne, après quelques manipulations algébriques, l'équation dynamique désirée :
![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] permettent d'évaluer :
] permettent d'évaluer :


![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] :
] :
![]() +
+ ![]() ), elle prend la forme :
), elle prend la forme :