


suivant: Développement de l'équation d'évolution
monter: Analyse linéaire de stabilité
précédent: Solution stationnaire uniforme
Table des matières
La perturbation du train de marches
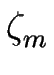 (x, t) peut se décomposer sur une base de Fourier :
(x, t) peut se décomposer sur une base de Fourier :
 (x, t) = (x, t) =    (t) eim (t) eim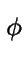 + iqx d + iqx d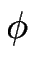 dq , dq ,
|
(B.8) |
où
 (t) est par définition la transformée de Fourier de
(t) est par définition la transformée de Fourier de
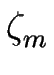 (x, t) par rapport aux variables x et m.
La variable m étant discrète, la variable associée
(x, t) par rapport aux variables x et m.
La variable m étant discrète, la variable associée 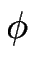 dans l'espace de Fourier peut être considérée comme une phase
dans l'espace de Fourier peut être considérée comme une phase
 [0, 2
[0, 2 ].
].
La réponse temporelle du train de marches est caractérisée par la pulsation  , variable conjuguée au temps t dans une transformation de Laplace ; on a alors :
, variable conjuguée au temps t dans une transformation de Laplace ; on a alors :
 (x, t) = (x, t) =     e e t + im t + im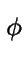 + iqx d + iqx d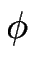 dq d dq d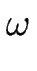 , ,
|
(B.9) |
où
 est la transformée de Laplace de
est la transformée de Laplace de
 (t) par rapport au temps.
L'intérêt d'une transformation de Laplace en temps est de pouvoir rendre compte de l'atténuation ou de l'amplification de la perturbation au cours du temps.
(t) par rapport au temps.
L'intérêt d'une transformation de Laplace en temps est de pouvoir rendre compte de l'atténuation ou de l'amplification de la perturbation au cours du temps.
Les différents modes ne se couplant pas dans une analyse linéaire, on étudiera la réponse  du système à un mode de Fourier (
du système à un mode de Fourier (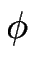 , q), soit :
, q), soit :
 (x, t) = (x, t) =  ewt + im ewt + im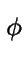 + iqx . + iqx .
|
(B.10) |
Les équations constitutives du modèle sont alors résolues ordre par ordre en
 . L'ordre
. L'ordre
 nous redonne la solution stationnaire et l'ordre
nous redonne la solution stationnaire et l'ordre
 permet de déterminer
permet de déterminer  , c'est-à-dire, la réponse linéaire du train de marches à la perturbation.
, c'est-à-dire, la réponse linéaire du train de marches à la perturbation.
 L'équation de diffusion sur les terrasses nous donne :
L'équation de diffusion sur les terrasses nous donne :
D  cm + F = 0 ; cm + F = 0 ;
|
(B.11) |
soit
D  + D + D    - D - D  q2 q2  cm1 + F = 0 , cm1 + F = 0 ,
|
(B.12) |
car

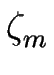 /
/ x = iq
x = iq 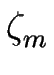 .
Le champ de concentration perturbé cm1 obéit donc à l'équation suivante :
.
Le champ de concentration perturbé cm1 obéit donc à l'équation suivante :
 - q cm1 = 0 ; - q cm1 = 0 ;
|
(B.13) |
dont la solution générale peut s'écrire :
cm1(z) = Am1 eq(z - m ) + Bm1 e-q(z - m ) + Bm1 e-q(z - m ) . ) .
|
(B.14) |
 Les équations aux limites (cf éq. [
Les équations aux limites (cf éq. [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]) vont nous permettre de déterminer les constantes d'intégration Am1 et Bm1.
]) vont nous permettre de déterminer les constantes d'intégration Am1 et Bm1.
L'équation cinétique [![[*]](crossref.gif) ] nous donne la première condition limite au niveau de la marche m :
] nous donne la première condition limite au niveau de la marche m :
    cm - cm -       cm cm![$\displaystyle \left.\vphantom{ \frac{}{} \partial_z c_m - \left(\varepsilon \partial_x \zeta_m \right) \, \partial_x c_m }\right]$](img1187.gif) (zm) (zm) |
= |
   cm(zm) - ceqm cm(zm) - ceqm![$\displaystyle \left.\vphantom{ \frac{}{} c_m(z_m) - c_{eq_m} }\right]$](img1189.gif) . . |
|
Par soucis de commodité, nous avons noté
 cm/
cm/ z par
z par
 cm.
cm.
En faisant usage de ce que :
| cm(zm) |
= |
cm0(zm) +   cm1(zm) cm1(zm) |
|
| |
= |
cm0(m ) + ) +    (m (m ) + ) +   cm1(m cm1(m ) + O( ) + O( ) . ) . |
(B.15) |
et en explicitant la concentration d'équilibre ceqm qui prend en compte l'énergie de courbure de la marche :
où  est la courbure de la marche m :
est la courbure de la marche m :
 |
= |
-  , , |
(B.17) |
d'où :
ceqm = ceq0  1 + 1 +  q2 q2 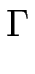   + O( + O( ) , ) , |
|
|
(B.18) |
la contribution d'ordre
 de l'équation [
de l'équation [![[*]](crossref.gif) ]
conduit alors à :
]
conduit alors à :
 cm0(m cm0(m ) + ) +  cm1(m cm1(m ) = ) =     cm0(m cm0(m ) + cm1(m ) + cm1(m ) - q2 ) - q2 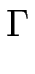 ceq0 ceq0![$\displaystyle \left.\vphantom{ \frac{}{} \partial_z c_m^0(m\ell) + c_m^1(m\ell) - q^2 \, \Gamma \, c_{eq}^0 }\right]$](img1198.gif) . . |
|
|
(B.19) |
Ceci nous donne finalement :
 q - q -   Am1 - Am1 -  q + q +   Bm1 = Bm1 =  , , |
|
|
(B.20) |
où nous avons posé :
L'équation cinétique [![[*]](crossref.gif) ] nous donne la deuxième condition limite :
] nous donne la deuxième condition limite :
    cm - cm -       cm cm![$\displaystyle \left.\vphantom{ \frac{}{} \partial_z c_m - \left(\varepsilon \partial_x \zeta_{m+1} \right) \, \partial_x c_m }\right]$](img1209.gif) (zm + 1) (zm + 1) |
= |
-    cm(zm + 1) - ceqm + 1 cm(zm + 1) - ceqm + 1![$\displaystyle \left.\vphantom{ \frac{}{} c_m(z_{m+1}) - c_{eq_{m+1}} }\right]$](img1211.gif) . . |
|
| |
|
|
(B.22) |
De même que précédemment, la concentration en bord de marche est développée au premier ordre en
 :
:
| cm(zm + 1) |
= |
cm0(zm + 1) +   cm1(zm + 1) cm1(zm + 1) |
|
| |
= |
cm0((m + 1) ) + ) +    ((m + 1) ((m + 1) ) + ) +   cm1((m + 1) cm1((m + 1) ) + O( ) + O( ) . ) . |
|
| |
|
|
(B.23) |
La concentration d'équilibre en bord de marche s'écrit quant à elle :
ceqm + 1 = ceq0  1 + 1 +  q2 q2 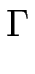   + O( + O( ) . ) . |
|
|
(B.24) |
Il reste à prendre en compte que
 = ei
= ei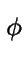
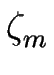 .
.
La contribution d'ordre
 de l'équation [
de l'équation [![[*]](crossref.gif) ]
conduit alors à :
]
conduit alors à :
ei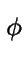  cm0((m + 1) cm0((m + 1) ) + ) +  cm1((m + 1) cm1((m + 1) ) ) |
= |
|
|
| |
|
-    ei ei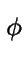  cm0((m + 1) cm0((m + 1) ) + cm1((m + 1) ) + cm1((m + 1) ) - q2 ei ) - q2 ei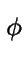 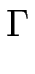 ceq0 ceq0![$\displaystyle \left.\vphantom{ \frac{}{} e^{i\phi} \, \partial_z c_m^0((m+1)\ell) + c_m^1((m+1)\ell) - q^2 \, e^{i\phi} \, \Gamma \, c_{eq}^0 }\right]$](img1217.gif) , , |
|
| |
|
|
(B.25) |
ce qui nous donne finalement :
 q + q +   eq eq Am1 - Am1 -  q - q -   e-q e-q Bm1 = ei Bm1 = ei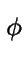  , , |
|
|
(B.26) |
où nous avons posé :
Les équations [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] nous permettent de déterminer les constantes Am1 et Bm1 :
] nous permettent de déterminer les constantes Am1 et Bm1 :
| Am1 = A1 |
= |
    q + q +   ei ei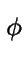  - -  q - q -   e-q e-q  ![$\displaystyle \left.\vphantom{ \frac{}{} \left(q + \frac{\nu_+}{D} \right)\, e^...
... \, \beta - \left( q - \frac{\nu_-}{D} \right) \, e^{-q\ell} \, \alpha }\right]$](img1225.gif) , , |
(B.28) |
| Bm1 = B1 |
= |
    q - q -   ei ei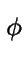  - -  q + q +   eq eq  ![$\displaystyle \left.\vphantom{ \frac{}{} \left(q - \frac{\nu_+}{D} \right)\, e^...
...} \, \beta - \left( q + \frac{\nu_-}{D} \right) \, e^{q\ell} \, \alpha }\right]$](img1227.gif) , , |
(B.29) |
où
 = 2 sh(q = 2 sh(q ) )  q2 + q2 +   + 2 + 2    + +   ch(q ch(q ) . ) . |
|
|
(B.30) |
 Finalement, la pulsation
Finalement, la pulsation  est déterminée par l'équation [
est déterminée par l'équation [![[*]](crossref.gif) ] de conservation de la masse aux marches. À l'ordre
] de conservation de la masse aux marches. À l'ordre
 , celle-ci conduit à :
, celle-ci conduit à :
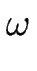 |
= |
 D D    cm0(m cm0(m ) + ) +  cm1(m cm1(m ) - ) -  cm - 10(m cm - 10(m ) - e-i ) - e-i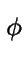  cm - 11(m cm - 11(m ) )![$\displaystyle \left.\vphantom{ \frac{}{} \partial_{z^2} c_m^0 (m\ell) + \partia...
...ial_{z^2} c_{m-1}^0(m\ell) - e^{-i\phi} \, \partial_z c_{m-1}^1(m\ell) }\right]$](img1235.gif) - a DL - a DL 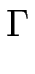 q4 , q4 , |
|
| |
|
|
(B.31) |
soit :
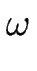 |
= |
 D D   q A1 - q B1 q A1 - q B1 - ei - ei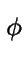  q eq q eq A1 - q e-q A1 - q e-q B1 B1 ![$\displaystyle \left.\vphantom{ \frac{}{} \left(q \, A^1 - q \, B^1 \right)
- e^{i\phi} \, \left( q \, e^{q\ell}\, A^1 - q \, e^{-q\ell} \, B^1 \right) }\right]$](img1241.gif) - a DL - a DL 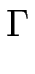 q4 . q4 . |
|
| |
|
|
(B.32) |
et, en utilisant les expressions de A1 et B1 :
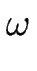 |
= |
2  D q2 ( D q2 ( - -  )sh(q )sh(q ) + 2 ) + 2  q ( q (  - -   ) ) ch(q ch(q ) - cos( ) - cos(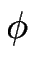 ) )![$\displaystyle \left.\vphantom{ {\rm ch}(q\ell) - _cos(\phi) }\right]$](img1243.gif) - a DL - a DL 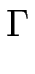 q4 q4 |
|
| |
+ |
2 i sin(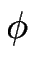 ) )  q ( q (  + +   ) . ) . |
(B.33) |
Après quelques manipulations algébriques nous obtenons :
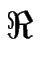 e( e(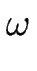 ) ) |
= |
- 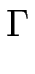 q2 q2   q2( q2( )sh(q )sh(q ) + 2 q( ) + 2 q( )(ch(q )(ch(q ) - cos( ) - cos(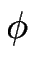 )) )) + a DL q2 + a DL q2![$\displaystyle \left.\vphantom{ \frac{2 \, D_S}{\Delta^1} \left( q^2 (\frac{\nu_...
...+\nu_-}{D^2}) ({\rm ch}(q\ell) - \cos(\phi)) \right) + a \, D_L \, q^2 }\right]$](img1250.gif) |
|
| |
|
+  F F        ( ( + +  ) )  q q sh(q sh(q ) + (cos( ) + (cos(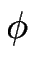 ) - ch(q ) - ch(q )) )) + +   q q sh(q sh(q ) )![$\displaystyle \left.\vphantom{ \frac{}{} (\nu_++\nu_-) \left( \frac{}{} \!\! q\...
...) + \frac{\nu_+\nu_-}{D} \, \frac{\ell}{2} \, q\ell \, {\rm sh}(q\ell) }\right]$](img1260.gif) , , |
|
| |
|
|
(B.34) |
 m( m(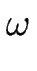 ) ) |
= |
i  F F  sin( sin(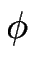 ) , ) , |
(B.35) |
où nous avons utilisé la constante de diffusion macroscopique
DS = 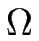 ceq0 D.
ceq0 D.
 En faisant usage des distances Schwoebel d+ et d- définies par , nous retrouvons les expressions présentées aux chapitre
En faisant usage des distances Schwoebel d+ et d- définies par , nous retrouvons les expressions présentées aux chapitre ![[*]](crossref.gif) :
:
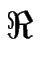 e( e(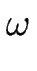 ) ) |
= |
- 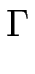 q2 q2 DS DS   2 2 ch(q ch(q ) - cos( ) - cos(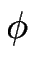 ) ) + q(d+ + d-) sh(q + q(d+ + d-) sh(q ) ) + a DLq2 + a DLq2![$\displaystyle \left.\vphantom{ D_S \, \frac{q}{{\cal D}} \left( 2 \left({\rm ch...
...(\phi) \right) + q(d_++d_-) \; {\rm sh}(q \ell) \right) + a \, D_L q^2 }\right]$](img187.gif) |
|
| |
|
+  F F     (d- + d+) (d- + d+) q q sh(q sh(q ) - ch(q ) - ch(q ) + cos( ) + cos(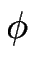 ) ) + +  q q sh(q sh(q ) )![$\displaystyle \left.\vphantom{ (d_-+d_+) \left( q \ell \; {\rm sh}(q \ell) - {\...
...ell) + \cos (\phi) \right) + \frac{\ell}{2} q \ell \; {\rm sh}(q \ell) }\right]$](img196.gif) , , |
|
| |
|
|
(B.36) |
 m( m(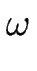 ) ) |
= |
 F sin( F sin(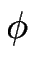 ) ) ( ( + d+ + d-), + d+ + d-), |
(B.37) |
où  est donné par :
est donné par :
 = (d+ + d-) q ch(q = (d+ + d-) q ch(q ) + (d+d- q2 + 1) sh(q ) + (d+d- q2 + 1) sh(q ) . ) .
|
(B.38) |



suivant: Développement de l'équation d'évolution
monter: Analyse linéaire de stabilité
précédent: Solution stationnaire uniforme
Table des matières
fred
2001-07-02
![]() (x, t) peut se décomposer sur une base de Fourier :
(x, t) peut se décomposer sur une base de Fourier :

![]() , variable conjuguée au temps t dans une transformation de Laplace ; on a alors :
, variable conjuguée au temps t dans une transformation de Laplace ; on a alors :


![]() du système à un mode de Fourier (
du système à un mode de Fourier (![]() , q), soit :
, q), soit :
![]() . L'ordre
. L'ordre
![]() nous redonne la solution stationnaire et l'ordre
nous redonne la solution stationnaire et l'ordre
![]() permet de déterminer
permet de déterminer ![]() , c'est-à-dire, la réponse linéaire du train de marches à la perturbation.
, c'est-à-dire, la réponse linéaire du train de marches à la perturbation.
![]() L'équation de diffusion sur les terrasses nous donne :
L'équation de diffusion sur les terrasses nous donne :
![]() Les équations aux limites (cf éq. [
Les équations aux limites (cf éq. [![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ]) vont nous permettre de déterminer les constantes d'intégration Am1 et Bm1.
]) vont nous permettre de déterminer les constantes d'intégration Am1 et Bm1.
![[*]](crossref.gif) ] nous donne la première condition limite au niveau de la marche m :
] nous donne la première condition limite au niveau de la marche m :
 ,
,![[*]](crossref.gif) ]
conduit alors à :
]
conduit alors à :
 .
.![[*]](crossref.gif) ] nous donne la deuxième condition limite :
] nous donne la deuxième condition limite :
![]() de l'équation [
de l'équation [![[*]](crossref.gif) ]
conduit alors à :
]
conduit alors à :
 +
+  .
.![[*]](crossref.gif) ] et [
] et [![[*]](crossref.gif) ] nous permettent de déterminer les constantes Am1 et Bm1 :
] nous permettent de déterminer les constantes Am1 et Bm1 :

![]() Finalement, la pulsation
Finalement, la pulsation ![]() est déterminée par l'équation [
est déterminée par l'équation [![[*]](crossref.gif) ] de conservation de la masse aux marches. À l'ordre
] de conservation de la masse aux marches. À l'ordre
![]() , celle-ci conduit à :
, celle-ci conduit à :
 )sh(q
)sh(q )(ch(q
)(ch(q
 sin(
sin(![]() En faisant usage des distances Schwoebel d+ et d- définies par , nous retrouvons les expressions présentées aux chapitre
En faisant usage des distances Schwoebel d+ et d- définies par , nous retrouvons les expressions présentées aux chapitre ![[*]](crossref.gif) :
:
