



suivant: Méthode de Newton-Raphson
monter: Méthodes numériques
précédent: Éléments finis
Table des matières
Nous ne considérerons que le cas des problèmes pouvant se ramener à une équation explicite du premier ordre en temps. À temps t fixé, la dérivée temporelle de f est alors fonction de f et de ses dérivées spatiales :
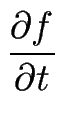 (t, x) = F (t, x) = F t, f, t, f,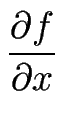 , ... , ... 
|
(D.18) |
La variable temporelle est traitée par un schéma de différences finies.
Indexons le temps discret par n ; l'instant t étant alors repéré par n, n + 1 représente l'instant t + dt et n - 1 l'instant t - dt.
Appelons fn la valeur de f à l'instant n et Fn celle de sa dérivée temporelle au même instant. Après le choix d'un schéma numérique pour les dérivées spatiales, Fn s'écrit comme un vecteur fonction de fn.
L'idée est d'écrire une relation entre f et ses dérivées aux instants précédents :
| |
|
 fn + 1 + b fn + c fn - 1 + d fn - 2 + ... fn + 1 + b fn + c fn - 1 + d fn - 2 + ... ![$\displaystyle \left.\vphantom{ f_{n+1} + b\,f_n + c\, f_{n-1} + d\, f_{n-2} + \cdots }\right]$](img1712.gif) |
|
| |
|
+ 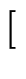 A Fn + 1 + B Fn + C Fn - 1 + D Fn - 2 + ... A Fn + 1 + B Fn + C Fn - 1 + D Fn - 2 + ... ![$\displaystyle \left.\vphantom{ A\,F_{n+1} + B\,F_n + C\,F_{n-1} + D\,F_{n-2} + \cdots }\right]$](img1714.gif) = 0 , = 0 , |
(D.19) |
compatible avec les développements de Taylor.
Ces méthodes nécessitant le stockage des valeurs de f et de ses dérivées aux instants antérieurs sont appelées « méthodes à pas multiples » .
On distingue deux types de schémas : ceux pour lesquels A = 0, appelés « schémas explicites » (la valeur de f à l'instant t + dt est déterminée explicitement en fonction des instants précédents) et ceux pour lesquels
A 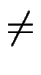 0, appelés « schémas implicites » qui nécessitent la résolution d'un système de N équations (où N est le nombre de noeuds du réseau numérique).
0, appelés « schémas implicites » qui nécessitent la résolution d'un système de N équations (où N est le nombre de noeuds du réseau numérique).
Si tous les coefficients sont nuls sauf b et B, on trouve le schéma d'Euler explicite :
|
fn + 1 = fn + dt Fn + O(dt2) .
|
(D.20) |
S'ils sont tous nuls sauf b et A, on obtient le schéma d'Euler implicite :
|
fn + 1 - dt Fn + 1 = fn + O(dt2) .
|
(D.21) |
La différence principale entre les deux types de schémas susmentionnés est la stabilité respective de chacun d'entre eux.
La stabilité d'un schéma numérique dépend du choix du schéma temporel mais aussi du schéma spatial choisi ainsi que du problème mathématique lui-même.
Les schémas explicites sont conditionnellement stables avec une condition de stabilité du type
dt <  hn, où dt est le pas de temps, h le pas du réseau, n l'ordre de la dérivée spatiale la plus élevée dans l'équation et
hn, où dt est le pas de temps, h le pas du réseau, n l'ordre de la dérivée spatiale la plus élevée dans l'équation et  un paramètre numérique qui dépend de l'équation elle-même.
Les schémas implicites sont plus stables et même souvent inconditionnellement stables (ou A-stables). Une étude quasi systématique de stabilité des schémas numériques a été effectuée par R. Piché [#!Piche95!#].
un paramètre numérique qui dépend de l'équation elle-même.
Les schémas implicites sont plus stables et même souvent inconditionnellement stables (ou A-stables). Une étude quasi systématique de stabilité des schémas numériques a été effectuée par R. Piché [#!Piche95!#].
Pour les différentes simulations numériques effectuées dans le cadre de cette thèse, nous avons choisi d'utiliser des schémas de type BDF ( « Backward Differentiation Formulae » ).
Ceux ci sont obtenus à partir de [![[*]](crossref.gif) ] en prenant les coefficients en lettre capitale, excepté A égaux à zéro.
Le schéma d'Euler implicite (BDF d'ordre 1) fait partie de cette famille ; il en est de même pour le « solver » de Gear (BDF d'ordre 2) :
] en prenant les coefficients en lettre capitale, excepté A égaux à zéro.
Le schéma d'Euler implicite (BDF d'ordre 1) fait partie de cette famille ; il en est de même pour le « solver » de Gear (BDF d'ordre 2) :
|
3fn + 1 - 2 dt Fn + 1 = 4fn - fn - 1 + O(dt3) .
|
(D.22) |
Les schémas de types BDF ont l'avantage d'être L-stables ; c'est-à-dire qu'en plus d'être A-stables (ou inconditionnellement stables), leur fonction de stabilité s'annule à l'infini : ils atténuent de façon optimale les hautes fréquences correspondant à du bruit numérique.
Ils conviennent parfaitement bien à la résolution numérique de l'équation dynamique du méandre (cf. chap. ![[*]](crossref.gif) ). Leur utilisation a permis de remédier aux erreurs d'intégration commises dans un travail antérieur [#!Pierre-Louis98a!#].
). Leur utilisation a permis de remédier aux erreurs d'intégration commises dans un travail antérieur [#!Pierre-Louis98a!#].
L'utilisation d'un schéma implicite conduit à la résolution d'une équation de la forme :
où fn + 1 est le vecteur à N (si N est le nombre de noeuds du réseau numérique) composantes représentant f à l'instant n + 1
et G est une fonction, dans notre cas, non linéaire.
Dans le cas du schéma de Gear [![[*]](crossref.gif) ], on a :
], on a :
|
G(fn + 1) = 3fn + 1 - 2 dt Fn + 1 - H ,
|
(D.24) |
où H est un vecteur à N composantes indépendant de fn + 1 :
|
H = 4fn - fn - 1 .
|
(D.25) |
Plusieurs méthodes de résolutions peuvent être envisagées.
Le choix de telle ou telle méthode dépendra essentiellement de la taille du système.
Sous-sections




suivant: Méthode de Newton-Raphson
monter: Méthodes numériques
précédent: Éléments finis
Table des matières
fred
2001-07-02
![[*]](crossref.gif) ] en prenant les coefficients en lettre capitale, excepté A égaux à zéro.
Le schéma d'Euler implicite (BDF d'ordre 1) fait partie de cette famille ; il en est de même pour le « solver » de Gear (BDF d'ordre 2) :
] en prenant les coefficients en lettre capitale, excepté A égaux à zéro.
Le schéma d'Euler implicite (BDF d'ordre 1) fait partie de cette famille ; il en est de même pour le « solver » de Gear (BDF d'ordre 2) :
![[*]](crossref.gif) ). Leur utilisation a permis de remédier aux erreurs d'intégration commises dans un travail antérieur [#!Pierre-Louis98a!#].
). Leur utilisation a permis de remédier aux erreurs d'intégration commises dans un travail antérieur [#!Pierre-Louis98a!#].
![[*]](crossref.gif) ], on a :
], on a :